ответ: 27 кв см
Условие задачи:
Периметр правильного треугольника, вписанного в окружность, равен 27 см. Найдите периметр и площадь правильного четырехугольника, описанного около этой же окружности.
Объяснение:
Найдем для начала, радиус вписанной окружности.
S=p*r, где полупериметр р=27/2= 13,5 см, а радиус r - нужно найти.
У правильного треугольника все стороны равны между собой а углы равны 60° . Так что медиана, КР является и биссектрисой и высотой. Любая сторона равна 27/3 = 9 см, следовательно из треугольника КРН
по определению косинуса
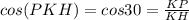
Отсюда КР = КН* cos 30 = 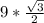
Значит площадь треугольника равна
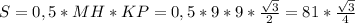
Значит 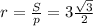
Из рисунка очевидно, что сторона квадрата равна диаметру окружности, то есть
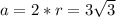
Площадь квадрата равна
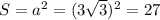 кв см
кв см
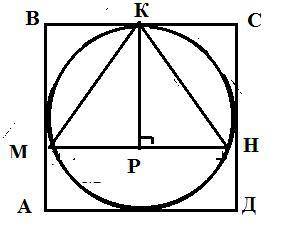
1) из того, что вд - медиана, - равенство площадей треугольников авд и свд.
2) из равенства площадей - равенство сторон ав и вс.
3) из равенства сторон - вд - не только медиана треугольника авс, но и биссектриса (угол авд = углу свд) и высота (вд перпендикулярна ас).
4) из перпендикулярности вд к ас треугольник авд - прямоугольный.
5) из отношения 1: 2 катета вд к гипотенузе ав - угол а=30 градусов.
6) из суммы углов треугольника = 180 градусов - угол авд = 60 градусов.
7) из 3) угол свд = 60 градусов.
8) найти угол fвс.
9) сравнить угол fвс с углом свд.
10) сделать вывод.
успеха!