При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°.
Что-то я засомневался и попробовал сам всё это получить.
Наклонная боковая сторона обозначена с, перпендикулярная основаниям - h;
Два очевидных соотношения.
c + h = a + b; (ну, раз можно вписать окружность)
c^2 - h^2 = (a - b)^2; (ну, если и это надо объяснять, то можно ничего не писать)
Делим второе на первое
с - h = (a - b)^2/(a + b);
Теперь это вычитаем из первого соотношения.
2*h = (a + b) - (a - b)^2/(a + b);(что-то я уже про корень сомневаюсь).
h = 2*a*b/(a + b); r = h/2 = a*b/(a + b);
А теперь - и не сомневаюсь, нет тут ни какого корня. А вот другая находка, и очень красивая - площадь такой (то есть прямоугольной, в которую можно вписать окружность) трапеции равна a*b
Важно так же и вот что - в пределе b -> 0 r не "превращается" в радиус вписанной окружности для прямоугольного треугольника - это совершенно разные вещи.
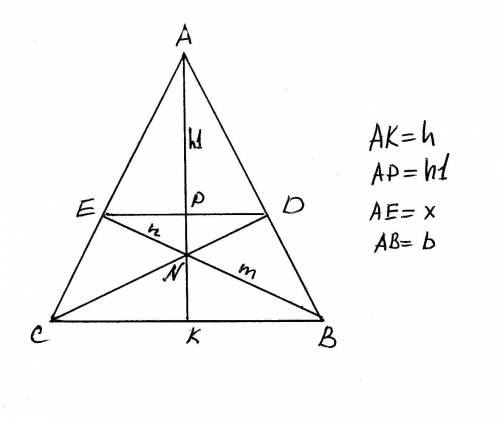
Все обозначения - на чертеже, посмотрите внимательно.
х/b = n/m (из того, что AN - биссектриса)
x/b = h1/h (из подобия треугольников APD и AKB)
NP/NK = n/m (из подобия EPN и NKB)
NK = h/4; NP = 3*h/4 - h1;
Итак, получили
h1/h = (3*h/4 - h1)/(h/4) = (3 - 4*h1)/h = 3 - 4*(h1/h);
h1/h = 3/5;
Пусть площадь АВС S, тогда
Площадь АСК = S/2; площадь CNK = (1/4)*(S/2) = S/8 (ну, я один раз это объясню - треугольники АСК и NCК имеют общую высоту СК и сторона КN = AК/4, поэтому площадь NCK = 1/4 от площади АСК)
Площадь ACN = 3*S/8;
Площадь АЕР = (3/5)^2 от площади АСК, поскольку это подобные треугольники, и стороны относятся, как 3/5, то есть площадь АЕР = (3/5)^2*(S/2).
Поэтому площадь четырехугольника EPNC равна 3*S/8 - (3/5)^2*(S/2); потом сосчитаем, пока же заметим, что нам осталось найти площадь треугольника NPD, которая равна (3/5)^2 от площади NCK (подобие и отношение сторон), то есть составляет (3/5)^2*S/8; собираем всё это, получаем, что искомая площадь треугольника CED, и, что то же самое - треугольника BED, равна
3*S/8 - (3/5)^2*(S/2) + (3/5)^2*S/8 = S*6/25;
Проверьте, может, я и налажал где :(((( но сам метод вроде правильный.
а можно и так, это побыстрее - Sаbе = S*3/5; Saed = (9/25)*S; Sbed = S*(3/5 - 9/25) =S*6/25. Значит, я не ошибся :))))
Ах, да, забыл на S на 20 заменить :))) Sbed = 6*20/25 = 24/5 = 4,8.
Пусть один (меньший) угол х, тогда второй х+20°. Сумма внутренних односторонних углов при двух параллельных прямых и секущей равна 180°. Составим уравнение :
х+х+20=180,
2х=160,
х=80° - меньший угол.