Дано: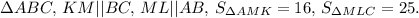 
Найти: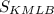 
Решение: Заметим, что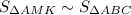 
по двум углам. Один угол общий, 
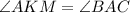- как односторонние углы при параллельных прямых КМ и ВС и секущей ВК.
Также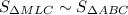 
по двум углам. Один угол общий, 
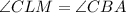- как односторонние углы при параллельных прямых LМ и AВ и секущей ВC.
Значит, по свойствам подобия треугольников
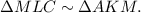
Вычислим коэффициент подобия этих треугольников
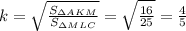
Заметим также, что
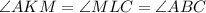- по свойству параллельных прямых.
По свойству параллелограмма ML=KB. По свойству подобия треугольников
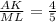
Пусть АК=4х, тогда КВ=ML=5x. AK+KB=AB=4x+5x=9x.
Значит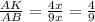 
- это коэффициент подобия треугольников AKM и AВС. Вычислим площадь теугольника АВС.
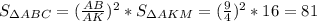
По своствам площадей
Подставим известные значения
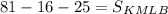
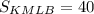
ответ: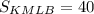
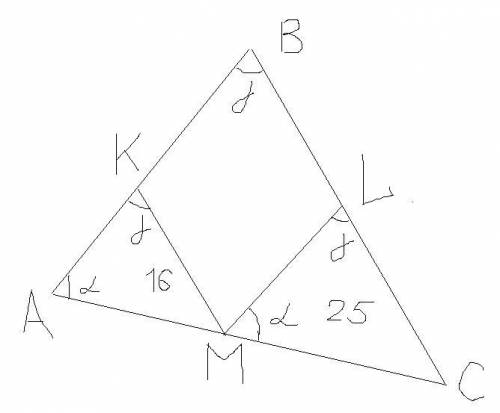
Оба треугольника 1 и 2 подобны исходному. Если какая-то (все равно - какая) сторона треугольника z, а соответственные ей стороны треугольников 1 и 2 - x и y, то
x + y = z; (это справедливо для любой стороны, но видно лучше всего, если z - основание) или x/z + y/z = 1;
Если обозначить S площадь всего треугольника, то S₁/S = (x/z)^2 и S₂/S = (y/z)^2; (площади подобных фигур пропорциональны квадратам линейных размеров, ну, скажем к примеру, - если сторона квадрата в 2 раза больше, то площадь - в 4, и так для любых подобных фигур - это теория, должны знать :))
Поэтому √(S₁/S ) + √(S₂/S) = 1; или S = (√S₁ + √S₂)^2 = (4 + 5)^2 = 81;
Отсюда площадь параллелограмма равна S - (S₁ + S₂) = 81 - (16 + 25) = 40;
ответ: 5cм - 1 основание
9 см - 2 основание
Объяснение: Средняя линия трапеции вычисляется по формуле:
ср.лин.= (a+b)/2, где a и b - основания трапеции.
Пусть 1 основание=X, тогда второе основание = X+4. Подставим данные значения в нашу формулу и получим:
7= (X+X+4)/2. Мы получили линейное уравнение с одной неизвестной. Решим его:
7*2=2X+4
14-4=2X
X=10/2
Х=5 - 1 основание
5+4=9 - 2 основание