Докажите, что угол между скрещивающимися прямыми, одна из которых содержит диагональ куба, а другая - диагональ грани куба, равен 90°.

решите подробно, .

👇

Увидеть ответ

Ответ:

GelyaKazarik

17.09.2020

Объяснение:

Вот

Докажите, что угол между скрещивающимися прямыми, одна из которых содержит диагональ куба, а другая

4,7(89 оценок)

Ответ:

арина1494

17.09.2020

Відповідь:

A1C и DB равен 90°.

Пояснення:

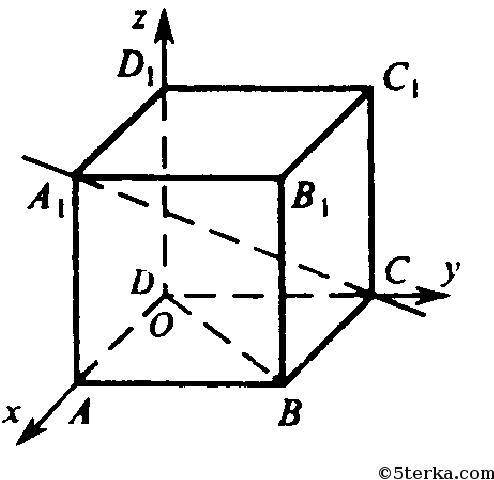
Пусть дан куб ABCDА1B1C1D1, А1С — диагональ куба; DB — диагональ грани куба.

Введем прямоугольную систему координат. С началом координат в т. D и осями, направленными вдоль ребер ОА, ОВ, ОС. Обозначим сторону куба через а.

https://ru-static.z-dn.net/files/db8/7fabd2e163d548ee435973a4d2fc01c5.png

Тогда

https://ru-static.z-dn.net/files/d03/960059a78aaeb368ff09035647522aff.png

https://ru-static.z-dn.net/files/d84/f0e867a68ec10485951a3ce407b94813.png

https://ru-static.z-dn.net/files/d65/90661f99b8c5653eccbb98e37e38d02e.png

Следовательно,

https://ru-static.z-dn.net/files/d73/59578781fa9cf36028faf845653e9834.png

соответственно угол между прямыми

A1C и DB равен 90°.

4,6(8 оценок)

Открыть все ответы

Ответ:

sotlen61Ang

17.09.2020

1. Чтобы решить эту задачу, нам нужно знать следующие факты о равнобедренном треугольнике:

- В равнобедренном треугольнике два угла при основании равны между собой, а угол при вершине больше этих двух углов при основании.

Поэтому, если угол при вершине в треугольнике равен 87°, то угол при основании будет меньше его.

Ответ: В равнобедренном треугольнике угол при основании будет меньше 87°.

2. Если в треугольнике NEG мы знаем, что угол N равен 6° и угол E равен 109°, то чтобы найти угол G, нужно использовать факт о сумме углов треугольника:

- Сумма углов треугольника равна 180°.

То есть, угол G = 180° - угол N - угол E.

Подставим известные значения в формулу:

угол G = 180° - 6° - 109° = 180° - 115° = 65°.

Ответ: Величина угла G равна 65°.

3. В данном вопросе нам дано, что отношение величин углов в треугольнике DRM составляет 2:1:3.

- Отношение величин углов в треугольнике можно представить как сумму значений коэффициентов:
угол D = 2x, угол R = x, угол M = 3x.

Используя факт о сумме углов треугольника (углы треугольника в сумме дают 180°), мы можем записать уравнение:
2x + x + 3x = 180°.

Скомбинируем коэффициенты:
6x = 180°.

Разделим обе стороны на 6:
x = 180° / 6 = 30°.

Теперь мы можем найти значение каждого угла:
угол D = 2x = 2 * 30° = 60°,
угол R = x = 30°,
угол M = 3x = 3 * 30° = 90°.

Ответ: Величина угла D равна 60°, угла R равна 30° и угла M равна 90°.

4. Чтобы решить эту задачу, нам нужно использовать факт о биссектрисе угла:

- Биссектриса угла делит данный угол на две равные части.

То есть, если ∠PMR = 69°, то угол ∠PRM тоже будет равен 69° (потому что PM равно PR, так как треугольник DRP равнобедренный).

Также, сумма углов в треугольнике равна 180°. Таким образом, мы можем найти последний угол треугольника:

угол ∠D = 180° - ∠P - ∠R = 180° - 69° - 69° = 180° - 138° = 42°.

Ответ: Величина угла D равна 42°, угла P равна 69° и угла R равна 69°.

4,7(21 оценок)

Ответ:

Bananthic

17.09.2020

Добрый день! Рад быть вашим учителем на сегодняшний урок математики.
Давайте рассмотрим задачу, которую вы мне задали. У нас есть наблюдатель на земле, который видит дерево под определенным углом. При движении дерева на некоторое расстояние, этот угол изменяется. Нам нужно найти высоту дерева и расстояние между наблюдателем и деревом.

Для начала, давайте визуализируем ситуацию. Представьте, что у вас есть треугольник: наблюдатель на земле, дерево и линия, соединяющая наблюдателя и верхушку дерева. Мы хотим найти два значения в этом треугольнике: высоту дерева и расстояние между наблюдателем и деревом.

Для удобства обозначим высоту дерева как "h" и расстояние между наблюдателем и деревом как "d". Имейте в виду, что эти значения являются неизвестными величинами, которые мы хотим найти.

Задача говорит нам, что при определенном угле видимости наблюдатель видит дерево под углом 45 °. Давайте обозначим этот угол как "alpha".
Теперь мы можем использовать тригонометрическую функцию синус для решения этой задачи. Синус угла определяется как отношение противоположной стороны к гипотенузе в прямоугольном треугольнике.

Используя это знание, мы можем записать следующее уравнение синуса для угла 45 °:
sin(45°) = h/d
Также известно, что угол видимости меняется на 60 °, когда дерево продвигается на расстояние 30 метров в сторону. Обозначим это новое расстояние как "d'". Мы можем записать еще одно уравнение синуса для угла 60 °:
sin(60°) = h/(d+d')
Обратите внимание, что второе уравнение имеет расстояние, равное сумме исходного расстояния и нового расстояния (d+d').

Теперь у нас есть два уравнения с двумя неизвестными переменными: h и d. Мы можем решить эту систему уравнений двумя способами: подставить одно уравнение в другое или использовать метод исключения или подстановки для изолирования неизвестных переменных.

Давайте решим задачу методом подстановки.
Из первого уравнения мы можем выразить h через d:
h = d*sin(45°)
Теперь подставим это значение h во второе уравнение:
sin(60°) = (d*sin(45°)) / (d+d')
Обратите внимание, что мы заменили h на выражение с d, потому что мы знаем, что h равно d*sin(45°).

Теперь мы можем решить это уравнение для d. Давайте продолжим:
sin(60°) = (d*sin(45°)) / (d+d')
Как уже известно, sin(45°) равен 1/√2 и sin(60°) равен √3/2. Подставим эти значения в уравнение:
√3/2 = (d*(1/√2)) / (d+d')

Для упрощения уравнения, давайте умножим его на 2 и избавимся от дробей:
√3 = (d*(1/√2)) / (d+d')
Умножим обе стороны уравнения на (d+d') и получим:
√3*(d+d') = d*(1/√2)
Раскроем скобки на левой стороне:
√3*d + √3*d' = d*(1/√2)
Далее, возьмем левую и правую части уравнения и изолируем переменные d и d':
√3*d - d/√2 = -√3*d'
Однако, нам нужно избавиться от √3 в знаменателе, чтобы получить более простую форму:
√2*√3*d - d = -√3*d'
Опустим знак "-", меняем местами переменные и упрощаем уравнение:
√2*√3*d + √3*d' = d

Теперь у нас есть система уравнений:
1) sin(45°) = h/d
2) √2*√3*d + √3*d' = d

Дальше нам нужно решить систему уравнений относительно неизвестных переменных h и d. Путем умножения уравнения №1 на d и подстановки в уравнение №2 мы получим:
(d*sin(45°)) * √2*√3 + √3*d' = d
Упростим это уравнение:
d*√2*√3*sin(45°) + √3*d' = d
Заметим, что sin(45°) равен 1/√2, поэтому заменим его в уравнении:
d*√2*√3 * (1/√2) + √3*d' = d
Упростим это уравнение еще больше:
d*√3 + √3*d' = d

Таким образом, мы получили новое уравнение:
√3*d + √3*d' = d

Обратите внимание, что это новое уравнение равносильно уравнению, которое мы получили ранее. Таким образом, мы можем сделать вывод, что для любого расстояния d и d', которые удовлетворяют условию задачи, мы и получим одинаковое значение для h и d.

Теперь мы можем решить это уравнение относительно d:
√3*d + √3*d' = d
Давайте приравняем левую и правую сторону уравнения:
√3*d + √3*d' = d
Уберем у кажого элемента √3:
d + d' = d
Вычтем d из обеих сторон уравнения:
d' = 0

Значение d' равно нулю, так как √3*d' = d, а если d'=0, то √3*d' также равно нулю. Это означает, что расстояние между наблюдателем и деревом не изменяется, когда оно движется в разных направлениях. Получается, что дерево находится прямо перед наблюдателем.

Давайте теперь найдем значение для h, используя первое уравнение:
sin(45°) = h/d
sin(45°) равен 1/√2, поэтому заменим его в уравнении:
1/√2 = h/d
Перемножим обе стороны уравнения на d, чтобы изолировать h:
h = d/√2
Используем это значение, чтобы найти h:
h = d/√2
Теперь мы знаем значение h в зависимости от значения d.

Итак, ответ на задачу:
а) Высота дерева составляет h = d/√2.
б) Расстояние между наблюдателем и деревом равно d.

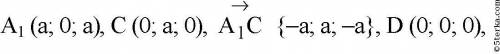
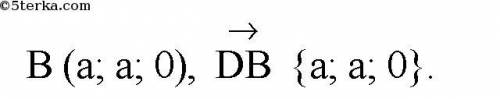
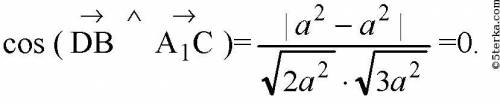
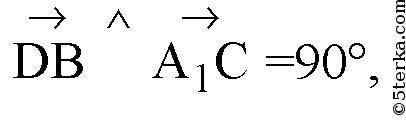
Надеюсь, что мое объяснение понятно и помогло вам понять решение задачи. Если у вас есть еще вопросы, не стесняйтесь задавать их.

4,6(55 оценок)

Это интересно:

Дом-и-сад

10.09.2020

Как установить в доме камеры наблюдения для системы безопасности...

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Кулинария-и-гостеприимство

02.02.2020

Как сделать красивые и вкусные французские макароны с миндалем...

Здоровье