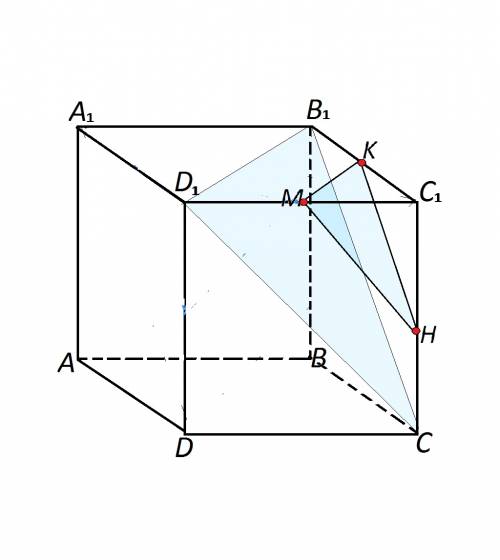
Сечение куба B1CD1 - треугольник, т.к. каждая пара его вершин принадлежит одной из граней.
Соответственно и сечение, проходящее через точку К и параллельное плоскости B1CD1 - также треугольник.
Так как его стороны параллельны диагоналям граней куба и проходят через их середины, они равны половине этих диагоналей.
Обозначим сечение МКН. Оно является равносторонним треугольником: МК=КН=МН.
Пусть стороны куба равны а см.
Тогда диагонали граней по формуле диагонали квадрата равны а√2, а стороны сечения МК=(а√2):2
ПлощадЬ правильного треугольника МКН
S=(МК²√3):4
S=(МК²√3):4=√3
S=((а√2):2)²*√3):4=√3
S=(2а²:4)*√3):4=√3
(а²:2)):4=1
а²:8=1
а²=8 - такова площадь одной грани куба.
S полной поверхности куба равна 6а²=8*6=48 см²
Нехай:
бiчна сторона = x,тодi основа = x-3
P — сума всiх сторiн,тому :
x+x+x-3=18
3x=21
x=7
Отже,бiчна сторона = 7 см ,тодi основа ∆ABC = х-3= 7-3 = 4см(AC=4cм)
У ∆ABC спiльна сторона AC з рiвностороннiм ∆ADC,тому P ∆ADC =
4+4+4=12 см.
Вiдповiдь: 12см.