A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
Четырёхугольник ABCD - равнобедренная трапеция (ВС║AD, AD > ВС, АВ = CD).
Отрезок ВН - высота, опущенная на основание AD (ВН⊥AD, ВН⊥ВС).
Отрезок МК - средняя линия.
AH : HD = 1 : 5.
HD = 35 см.
Найти :МК = ?
Решение :На основание AD из вершины тупого ∠С опустим высоту СН₁ (СН₁⊥AD, СН₁⊥ВС).
По свойству отрезков в равнобедренной трапеции, образованных основанием высоты на большем основании :
АН = DH₁.
Пусть АН = х, тогда, по условию задачи, HD = 5х.
HD = 5х
35 см = 5х
х = 35 см/5
х = 7 см.
АН = DH₁ = х = 7 см
AD = AH + HD = 7 см + 35 см = 42 см.
Рассмотрим четырёхугольник BHH₁C.
Все его углы прямые, значит, этот четырёхугольник - прямоугольник (признак прямоугольника).
AD = AH + HH₁ + DH₁
HH₁ = AD - AH - DH₁ = 42 см - 7 см - 7 см = 28 см.
Тогда ВС = НН₁ = 28 см (так как противоположные стороны прямоугольника равны).
Средняя линия трапеции равна полусумме её оснований.Следовательно :
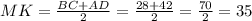 cм.
cм.
ответ :35 см.