Функции Excel:
1. КОРЕНЬ (число) - получаем значение квадратного корня (число>0)
=КОРЕНЬ(2,25) → 1,5
2. НОД (число1; число2) - получаем наибольший общий делитель (наибольшее целое число, на которое делятся число1 и число2 без остатка) двух (можно нескольких) целых чисел (число1>0, число2>0)
=НОД(45; 12) → 3
3. НОК (число1; число2) - получаем наименьшее общее кратное (наименьшее целое число, которое делится на число1 и число2 без остатка) двух (можно нескольких) целых чисел (число1>0, число2>0)
=НОК(12; 5) → 60
4. ОКРУГЛ (число; количество разрядов) - получаем число округлённое до указанного количества разрядов (количество разрядов = 0 - округляется до ближайшего целого; количество разрядов > 0 - округляется до указанного количества дробных разрядов - десятых, сотых и т.д.; количество разрядов < 0 - округляется до указанного количества целых разрядов - десятков, сотен и т.д.)
=ОКРУГЛ(1,573; 0) → 2
=ОКРУГЛ(1,573; 2) → 1,57
=ОКРУГЛ(15,73;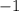 
) → 20
5. ОСТАТ (число; делитель) - получаем остаток от деления числа на делитель, полученное число имеет тот же знак, что и делитель (делитель ≠ 0)
=ОСТАТ(7; 5) → 2
=ОСТАТ(5; 7) → 5
=ОСТАТ(7; 7) → 0
6. РИМСКОЕ (число) - получаем из арабского числа римское в текстовом формате (число>0)
=РИМСКОЕ(2020) → MMXX
Объяснение:
Вместо число можно указывать ссылку на ячейку
Многочленом называется сумма одночленов.
Многочленом является 3x2y −7xy .
Многочленом также является 3x2y+(−7yx)=3x2y−7yx .
Одночлены, из которых состоит многочлен, называются членами многочлена.
Членами многочлена 2x2y+3xy−2 являются 2x2y , 3xy и −2 .
Записать коэффициенты и степени членов многочлена 4a2b−ba+12 .
Члены многочлена
4a2b
−ba
12
Коэффициенты членов
4
−1
12
Степени членов
3
2
0
Если коэффициент не указан, его значение равно 1 .
Члены многочлена называются подобными, если их переменные множители равны.
Подобные члены многочлена складываются, при сложении подобных членов их коэффициенты складываются.
Подобными членами многочлена 3x2y+2x2y−2xy+yx2+4−3 являются 3x2y;2x2y;yx2 .
Подобными являются также 4 и −3 , у которых переменных множителей вообще нет.
Сложив все подобные члены многочлена, получаем:
3x2y¯¯¯¯¯¯¯+2x2y¯¯¯¯¯¯¯−2xy+yx2¯¯¯¯¯+4−3 = 6x2y−2xy+1
(легче выполнять действия, если подчеркнуть подобные члены).
Многочлен записан в стандартном виде, если все подобные члены сложены и записаны в стандартном виде.
Записать многочлен 6+10x2yx−6xyx⋅x+3x2y−4 в стандартном виде:
1. записываются члены многочлена в стандартном виде.
6+10x2yx¯¯¯¯¯¯¯¯¯¯¯−6xyx⋅x¯¯¯¯¯¯¯¯¯¯¯+3x2y−4=6+10x3y−6x3y+3x2y−4=
2. Находятся подобные члены.
=6¯¯+10x3y¯¯¯¯¯¯¯¯−6x3y¯¯¯¯¯¯¯+3x2y−4¯¯=
3. Вычитаются (cуммируются) подобные члены многочлена 6−4=2 и 10−6=4 .
=2+4x3y+3x2y=
4. Члены многочлена можно упорядочить в порядке убывания степеней:
=4x3y+3x2y+2 .
Степенью многочлена в стандартном виде называется наибольшая из степеней входящих в него одночленов.
Определить степень многочлена 3a4b2−2a3b2+ab2−ab+2 .
Члены многочлена
3a4b2 −2a3b2 a1b2 −a1b1 2a0
Степень членов многочлена
4+2=6
3+2=5
1+2=3
1+1=2 0
Данный многочлен является многочленом шестой степени.