8D
Объяснение:
1) Решение по простому. Шестнадцатиричная система это 4 бита на один знак. У нас двоичная запись 10001101. Всего 8 бит. Значит младшие 4 бита это младшее шестнадцатиричное число, а старшие 4 бита это старшее число. Смотрим на первые 4 бита 1101 это 1*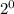 +0*
+0*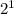 +1*
+1*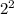 +1*
+1*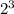 =1*1+0*2+1*4+1*8=1+4+8=13(в десятичной)=D (A-10, B-11, C-12, D-13 в 16-ричной).
=1*1+0*2+1*4+1*8=1+4+8=13(в десятичной)=D (A-10, B-11, C-12, D-13 в 16-ричной).
Смотрим на старшую четверку битов 1000=0*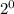 +0*
+0*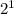 +0*
+0*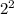 +1*
+1*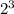 =0+0+0+8=8.
=0+0+0+8=8.
Пишем старшую цифре потом младшую 8D.
2)Теперь решение как нужно делать правильно (для любого основания). 10001101=1*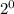 +0*
+0*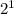 +1*
+1*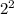 +1*
+1*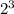 +0*
+0*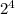 +0*
+0*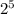 +0*
+0*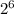 +1*
+1*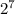 =1*1+0*2+1*4+1*8+0*16+0*32+0*64+1*128=1+4+8+128=141 (это перевели в десятичную). Затем переводим в нужную нам 16-ричную (это основание 16 значит будем делить на 16). 141/16= 8,8125. Мы получили целую часть от деления - цифра 8. Она у нас будет старшей (если при первом делении получилось число больше основания т.е.16 нужно его еще разделить). Умножим 8 на основание и вычтим это число из первоначального. 141-8*16=141-128=13. Мы получили младший разряд. Переводим 13 в 16-ричную (как показал ранее А-10 и т.д.). Получили ответ 8D
=1*1+0*2+1*4+1*8+0*16+0*32+0*64+1*128=1+4+8+128=141 (это перевели в десятичную). Затем переводим в нужную нам 16-ричную (это основание 16 значит будем делить на 16). 141/16= 8,8125. Мы получили целую часть от деления - цифра 8. Она у нас будет старшей (если при первом делении получилось число больше основания т.е.16 нужно его еще разделить). Умножим 8 на основание и вычтим это число из первоначального. 141-8*16=141-128=13. Мы получили младший разряд. Переводим 13 в 16-ричную (как показал ранее А-10 и т.д.). Получили ответ 8D
begin
if (((k mod 2=0) and (l mod 2<>0)) or ((l mod 2=0) and (k mod 2<>0)))=(((m mod 2=0) and (n mod 2<>0)) or ((n mod 2=0) and (m mod 2<>0))) then first:=true else first:=false;
end;
2)function second(k,l,m,n:integer):boolean;
begin
if (k=m) or (l=n) or (((k+1)=m) and ((l+1)=n)) or (((k+2)=m) and ((l+2)=n)) or (((k+3)=m) and ((l+3)=n)) or (((k+4)=m) and ((l+4)=n)) or (((k+5)=m) and ((l+5)=n)) or (((k+6)=m) and ((l+6)=n)) or (((k-1)=m) and ((l-1)=n)) or (((k-2)=m) and ((l-2)=n)) or (((k-3)=m) and ((l-3)=n)) or (((k-4)=m) and ((l-4)=n)) or (((k-5)=m) and ((l-5)=n)) or (((k-6)=m) and ((l-6)=n)) or (((m+1)=k) and ((n+1)=l)) or (((m+2)=k) and ((n+2)=l)) or (((m+3)=k) and ((n+3)=l)) or (((m+4)=k) and ((n+4)=l)) or (((m+5)=k) and ((n+5)=l)) or (((m+6)=k) and ((n+6)=l)) or (((m-1)=k) and ((n-1)=l)) or (((m-2)=k) and ((n-2)=l)) or (((m-3)=k) and ((n-3)=l)) or (((m-4)=k) and ((n-4)=l)) or (((m-5)=k) and ((n-5)=l)) or (((m-6)=k) and ((n-6)=l)) or (((k-1)=m) and ((l+1)=n)) or (((k-2)=m) and ((l+2)=n)) or (((k-3)=m) and ((l+3)=n)) or (((k-4)=m) and ((l+4)=n)) or (((k-5)=m) and ((l+5)=n)) or (((k-6)=m) and ((l+6)=n)) or (((k-1)=m) and ((l+1)=n)) or (((k-2)=m) and ((l+2)=n)) or (((k-3)=m) and ((l+3)=n)) or (((k-4)=m) and ((l+4)=n)) or (((k-5)=m) and ((l+5)=n)) or (((k-6)=m) and ((l+6)=n)) or (((m-1)=k) and ((n+1)=l)) or (((m-2)=k) and ((n+2)=l)) or (((m-3)=k) and ((n+3)=l)) or (((m-4)=k) and ((n+4)=l)) or (((m-5)=k) and ((n+5)=l)) or (((m-6)=k) and ((n+6)=l)) or (((m-1)=k) and ((n+1)=l)) or (((m-2)=k) and ((n+2)=l)) or (((m-3)=k) and ((n+3)=l)) or (((m-4)=k) and ((n+4)=l)) or (((m-5)=k) and ((n+5)=l)) or (((m-6)=k) and ((n+6)=l)) then second:=true else second:=false;
end;