Сначала переводим числа 6 и 4 в 2-ную систему. Для этого делим всё время на 2 с остатком:
6 / 2 = 3 (остаток 0)
3 / 2 = 1 (остаток 1)
Выписываем последний результат деления (1) и все остатки, начиная с конца:
1 1 0
Таким образом:
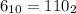
Аналогично:
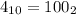
Умножаем: 110 х 100 = 11000
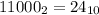
Тут действует такое же правило, что и для обычных десятичных чисел: чтобы умножить на 10, 100, 1000, 10000 и т.д., достаточно просто дописать справа столько нулей, сколько их есть в этом множителе. А вобще умножение двоичных чисел выполняется точно так же, как и десятичных - если нужно, то в столбик. Двоичную "Таблицу умножения" очень легко выучить наизусть:
0 х 0 = 0
0 х 1 = 0
1 х 0 = 0
1 х 1 = 1
Когда при умножении в столбик мы складываем промежуточные результаты, правила тоже простые:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 0
1 + 1 = 10
(смотри пример умножения на прикреплённом рисунке)
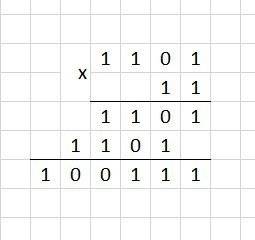
признаком разветвляющегося алгоритма является наличие операций проверки условия. различают два вида условий – простые и составные.
простым условием (отношением) называется выражение, составленное из двух арифметических выражений или двух текстовых величин (иначе их еще ), связанных одним из знаков:
< - меньше,
> - больше,
< = - меньше, или равно
> = - больше, или равно
< > - не равно
= - равно
например, простыми отношениями являются следующие:
x-y> 10; k< =sqr(c)+abs(a+b); 9< > 11; ‘мама’< > ‘папа’.
в примерах первые два отношения включают в себя переменные, поэтому о верности этих отношений можно судить только при подстановке некоторых значений:
если х=25, у=3, то отношение x-y> 10 будет верным, т.к. 25-3> 10
если х=5, у=30, то отношение x-y> 10 будет неверным, т.к. 5-30< 10
проверьте верность второго отношения при подстановке следующих значений:
а) k=5, a=1, b=-3, c=-8
b) k=65, a=10, b=-3, c=2