54 тройки.
Объяснение:
Я не придумал ничего умнее, чем просто выписать все 20 членов этой последовательности.
20-ый член оказался чудовищным набором цифр:
1113.122113.121113.222123.21121113.12111213.111213.21123.113.213.221121113.122113.12112
213.21123.113.213.221121113.122113.11123.113.3.221121113.122113.121113.22111213.1221123.
13.11123.1121123.22211213.2113.213.22113.3.11213.2113.2213.21123.113.11222113.2213.2
11213.123.21123.113.112221121113.121113.121113.123.1121123.22111213.2113.22213.12113.211
Нетрудно подсчитать, что троек здесь 54 штуки.
1. Число не меньше 50 и четное: 50
2. Опечатка, вероятно. Либо наибольшее X - тогда 99, либо наименьшее натуральное x, и тогда это будет 1, либо НЕ меньше 100, тогда 101
3. Немного запутано, но по идее: число должно быть четным и меньше 10. Максимальное такое число: 8
4. X больше либо равен 7, или x меньше 6. Единственное число, которое НЕ подходит под эту формулу: 6
10. Обычное уравнение вида 
При том что n только натурален. Очевидно, что n = 2
17. Надо просмотреть каждую пару чисел и поставить плюсик, если первое больше 15 или второе больше 9. Я загнул пять пальцев, лучше меня перепроверить
25. У эсминца всего 2500 из которых 500 принадлежат также и фрегату. А всего-всего их 4500. Значит ТОЛЬКО эсминцу принадлежат 2000, ТОЛЬКО фрегату тоже 2000, а фрегату всего 2000+500 = 2500. Я понимаю, что ничего из этой писанины понять невозможно, так что прилагаю картиночку, написанную замороженной куриной лапой.
45. Столько писанины, а проще взять листочек в клеточку и самому побыть роботом, исполняя команды. Если у меня все верно, то за один цикл получается общее смещение на 1 вверх и 1 вправо. Значит за 5 циклов будет смещение (5,5) и чтоб переместиться в начало надо дать команду (-5,-5)
53. Третья строчка аналогична: a = 2*4 + 7*3. Любой второклассник скажет, что это 29. Четвертая строчка аналогична: b = 30-29 = 1. Таким образом, у нас a = 29, b = 1. А просят найти именно b. В ответ пишем 1
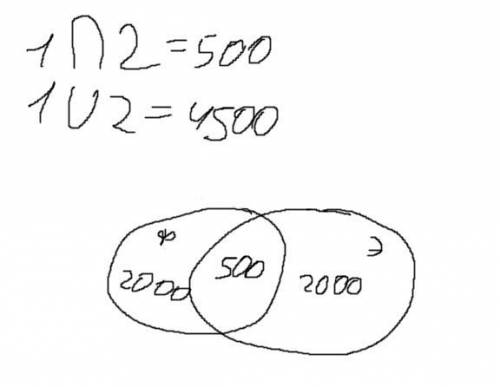
Объяснение:
x y z (-x или -y или z)
0. 0. 0. 1
0. 0. 1. 1
0. 1. 0. 1
0. 1. 1. 1
1. 0. 0. 1
1. 0. 1. 1
1. 1. 0. 0
1. 1. 1. 1