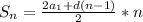
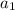- это член последовательности с индексом 1, то есть первое число в ряду. 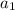= 1 (в условии задачи сказано что первый подарок весит 1кг)
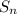- это сумма веса всех подарков, в примере используется слово "weight" что в переводе "вес", поэтому подставим это слово.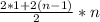
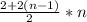
( Решение на Pascal )
Не совсем ясно, каким образом составители задачи планировали найти среди случайных вещественных 10 чисел в диапазоне от -60 до 100 числа, кратные 8.
Но ради Бога:
var A: array [1..10] of real;
var i,s: integer;
begin
s:=0;
randomize();
for i:=1 to 10 do
begin
A[i]:=random()*160-60;
write(A[i]:3:5,' ');
if (A[i]>10) and (A[i]-trunc(A[i])=0)
and (trunc(A[i]) mod 8 =0) then
s:=s+1;
end;
writeln();
writeln('Количество элементов массива,',
'кратных числу 8 и больших 10: ',s);
end.