4. 14
9. 5
Объяснение:
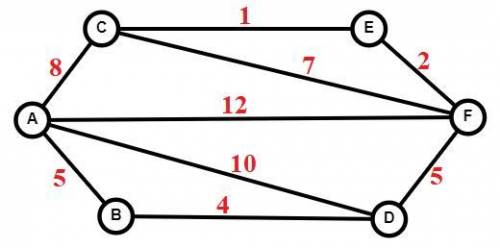
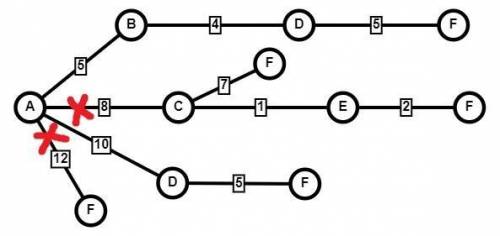
4. построим граф (картинка 1) или дерево (картинка 2, вычеркнуты пути, которые не приводят в D)
По ним видно, что добраться из A в F через D можно 2 путями, посчитаем их длину
ADF = 10 + 5 = 15
ABDF = 5 + 4 + 5 = 14
Длина кратчайшего пути между пунктами A и F, проходящий через пункт D, равна 14
9. картинка 3
Т.к. по условию нам нужны пути не проходящих через город D, то вычеркнем все пути ведущие в D (AD) и из него (DG и DE)
Начала пути (A) всегда 1 путь
A = 1
Дальнейшее количество путей - сумма от входящих путей (стрелочек).
Вычеркнутые пути НЕ считаем.
B = A = 1
E = A = 1 (DE вычеркнут)
и т.д.
Существует 5 различных путей из города A в город H, не проходящих через город D

Вычитание выполнено в шестеричной системе счисления.
Объяснение:
Мы видим в данном выражении цифры до 4. Из этого следует, что система счисления использует не менее 5 цифр. То есть, она как минимум - пятиричная. Будем подбирать по порядку системы счисления и вычислять их значения.
Пятиричная система счисления:
1. Переводим в десятичную систему счисления:
102 = 25 * 1 + 5 * 0 + 1 * 2 = 25 + 0 + 2 = 27
14 = 5 * 1 + 1 * 4 = 5 + 4 = 9
2. Вычисляем в десятичной системе счисления:
27 - 9 = 18
3. Переводим в пятиричную систему счисления:
18 = 33
Вывод: данная система счисления не подходит.
Шестеричная система счисления:
1. Переводим в десятичную систему счисления:
102 = 36 * 1 + 6 * 0 + 1 * 2 = 36 + 0 + 2 = 38
14 = 6 * 1 + 1 * 4 = 6 + 4 = 10
2. Вычисляем в десятичной системе счисления:
38 - 10 = 28
3. Переводим в шестеричную систему счисления:
28 = 44
Вывод: данная система счисления подходит.
УДАЧИ! ОБРАЩАЙТЕСЬ!