Question

Найти тангенсы внутренних углов треугольника abc с вершинами в точках
а(1; 2) в(11; -3) с(7; 5)

Answer 1

$tgA=\frac{4}{3}\\tgB=-\frac{3}{4}\\tgC$ - не определен (C=90°)

Пошаговое объяснение:

1) Получим уравнения трех прямых треугольника по формуле для прямой, проходящей через две точки:

$\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}$

Первая пара точек A,B:

$l_{1}: \frac{x-1}{11-1}=\frac{y-2}{-3-2}$ ⇒ $\frac{x-1}{10}=\frac{y-2}{-5}$

Приведем уравнение к виду:

$y=kx+b$

$\frac{x-1}{10}=\frac{y-2}{-5}$ ⇒ $y=-\frac{1}{2}x+\frac{5}{2}$

Вторая пара точек А,С:

$l_{2}: \frac{x-1}{7-1}=\frac{y-2}{5-2}$ ⇒ $\frac{x-1}{6}=\frac{y-2}{3}$

⇒ $y=\frac{1}{2}x+\frac{3}{2}$

Третья пара точек B,C:

$l_{3}: \frac{x-11}{7-11}=\frac{y-(-3)}{5-(-3)}$ ⇒ $\frac{x-11}{-4}=\frac{y+3}{8}$ ⇒ $y=-2x+19$

---

Теперь найдем тангенсы углов по формуле:

$tga=\frac{k2-k1}{1+k1k2}$ , где $k1 \ , \ k2$ - коэффициенты в уравнении прямых.

tgA - угол между прямыми AB и AC ($l_{1}$ и $l_{2}$):

$tgA=\frac{k2-k1}{1+k1k2}=\frac{\frac{1}{2}-(-\frac{1}{2})}{1+(-\frac{1}{2})\cdot \frac{1}{2}}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$

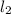tgB - угол между прямыми AB и BC ($l_{1}$ и $l_{3}$):

$tgB=\frac{k2-k1}{1+k1k2}=\frac{-2-(-\frac{1}{2})}{1+(-\frac{1}{2})\cdot -2}=\frac{-1,5}{2}=-\frac{3}{4}$

tgC - угол между прямыми AC и BC (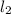$l_{2}$ и $l_{3}$):

$tgC=\frac{k2-k1}{1+k1k2}=\frac{-2-\frac{1}{2}}{1+\frac{1}{2}\cdot (-2)}=\frac{-2,5}{0}\\$

Здесь 0 в знаменателе означает, что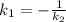 $k_{1}=-\frac{1}{k_{2}}$, а это условие перпендикулярности прямых. То есть угол C равен 90°.