Question

Знайдить уси пары такых натуральных чысел х та у що ( нсд(х,у))2=ху

Answer 1

Для всех равных пар натуральных чисел

Пошаговое объяснение:

Пусть канонические виды чисел x и y таковы:

$x=p_{1}^{\alpha_{1}}*p_{2}^{\alpha_{2}}*p_{3}^{\alpha_{3}}*...*p_{k}^{\alpha_{k}}$

$y=p_{1}^{\beta_{1}}*p_{2}^{\beta_{2}}*p_{3}^{\beta_{3}}*...*p_{k}^{\beta_{k}}$

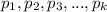где $p_{1}, p_{2}, p_{3}, ..., p_{k}$  - простые числа, а

$\alpha_{1}}, \alpha_{2}, \alpha_{3}, ...,\alpha_{k}, \beta_{1}}, \beta_{2}, \beta_{3}, ...,\beta_{k}$ - целые неотрицательные степени простых чисел (некоторые могут равняться нулю).

Тогда по свойству НОД(x; y)=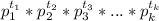$p_{1}^{t_{1}}*p_{2}^{t_{2}}*p_{3}^{t_{3}}*...*p_{k}^{t_{k}$

где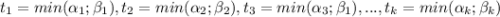 $t_{1}}=min(\alpha _{1}; \beta_{1}), t_{2}}=min(\alpha _{2}; \beta_{2}), t_{3}}=min(\alpha _{3}; \beta_{1}), ..., t_{k}}=min(\alpha _{k}; \beta_{k})$

По условию НОД(x; y)²=x · y и отсюда следует, что

$2t_{1}}=\alpha _{1}+\beta_{1}, 2t_{2}}=\alpha _{2}+\beta_{2}, 2t_{3}}=\alpha _{3}+\beta_{1}, ..., 2t_{k}}=\alpha _{k}+\beta_{k}$

Очевидно, что значение min(m; n) или m или n. Поэтому, если

$min(\alpha _{1}; \beta_{1})=\alpha _{1}$ , то из равенства $2t_{1}}=\alpha _{1}+\beta_{1}$ следует, что $2\alpha _{1}=\alpha _{1}+\beta_{1}$ и $\alpha _{1}=\beta _{1}$. Точно такое равенство можно установить если $min(\alpha _{1}; \beta_{1})=\beta_{1}$ .

И такие равенства получаются для других степеней простых чисел.

Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.

Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.