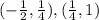`1) Если в треугольниках основания равны, а высота общая, то площади таких треугольников равны. См. рисунок в приложении. Δ B₁MC₂ и Δ B₁C₂C имею равные основания МС₂=С₂С и общую высоту, проведенную из точки В₁ на МС. S (Δ B₁MC₂)=S( Δ B₁C₂C) Аналогично S (Δ А₁MC₂)=S( Δ А₁C₂C) S (Δ А₁MВ₂)=S( Δ А₁В₂В) S (Δ С₁MВ₂)=S( Δ С₁В₂В) S (Δ С₁MА₂)=S( Δ С₁А₂А) S (Δ B₁MА₂)=S( Δ B₁А₂А)
2) По свойству средней линии треугольника А₂В₁=А₁В₂=СС₁/3 А₂С₁=С₂А₁=ВВ₁/3 В₂С₁=С₂В₁=АА₁/3
По формуле нахождения медианы треугольника через стороны ( легко получается из формулы: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон)
ответ: Увеличение на: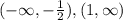
Убывает на: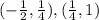 .
.
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1, .
.
1, .
.
Выясним, при каких значениях переменной функция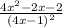 не определена.
не определена.
Разобьем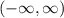 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала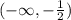 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на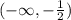 , так как
, так как 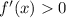 .
.
Подставим значение из интервала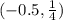 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на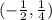 , поскольку
, поскольку 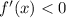
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на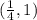 , поскольку
, поскольку 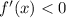
Подставим значения из интервала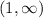 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на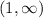 , так как
, так как 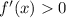 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: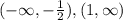
Убывает на: