![\sqrt[3]{75} - \sqrt[3]{3} * (\sqrt[3]{5})^{2} + \frac{13}{\sqrt[3]{49} - \sqrt[3]{42} + \sqrt[3]{36}} - \sqrt[6]{49} - \sqrt[6]{36} = \sqrt[3]{75} - \sqrt[3]{75} + \frac{13 * (\sqrt[3]{7} + \sqrt[3]{6})}{(\sqrt[3]{7^{2}} - \sqrt[3]{7} * \sqrt[3]{6} + \sqrt[3]{6^{2})} * (\sqrt[3]{7} + \sqrt[3]{6)}} - \sqrt[3]{7} - \sqrt[3]{6} = \frac{13 * (\sqrt[3]{7} + \sqrt[3]{6}) }{(\sqrt[3]{7})^{3} + (\sqrt[3]{6})^{3}} - \sqrt[3]{7} - \sqrt[3]{6} = \frac{13 * (\sqrt[3]{7} + \sqrt[3]{6}) }{13} - \sqrt[3]{7} - \sqrt[3]{6} = \sqrt[3]{7} + \sqrt[3]{6} - \sqrt[3]{7} - \sqrt[3]{6} = 0](/tpl/images/1012/8396/e6516.png)
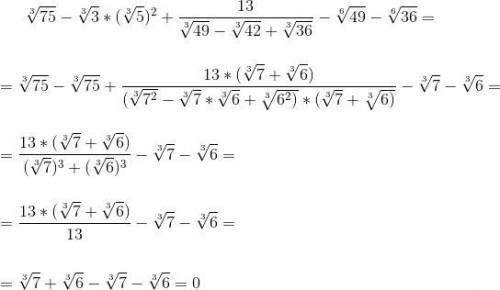
Пошаговое объяснение:
1 коробка = х конфет
2 коробка = у конфет
х + у = 64
3(х - 10) = у + 10
х + у = 64
3х - 30 = у + 10
х + у = 64
3х - у = 10 + 30
х + у = 64
3х - у = 40
Решим систему методом сложения:
4х = 104
х + у = 64
1)
4х = 104
х = 104 : 4
х = 26
2)
х + у = 64
26 + у = 64
у = 64 - 26
у = 38
1 коробка = (х) = 26 конфет было первоначально
2 коробка = (у) = 38 конфет было первоначально
26 - 10 = 16 - стало в 1 коробке
38 + 10 = 48 - стало во 2 коробке
48 : 16 = 3 (раза) - меньше в 1
38 конфет = 100%
26 конфет = х %
38/26 = 100/х
х = 26 * 100 / 38
х = 2600/38
х = 68. 16/38
х = 68. 8/19
26 конфет = 68. 8/19 %
100 - 68. 8/19 =
99. 19/19 - 68. 8/19 =
31. 11/19 % - было меньше в 1 коробке изначально
ответ: на 31. 11/19 % меньше