1) x²−7x−8 < 0
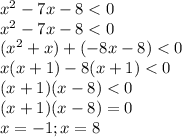
Определяем знаки на промежутках:
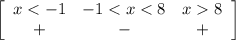
Интервал −1 < x < 8 — удовлетворяет неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−1; 8).
2) 3x²−4x+7 ≥ 0
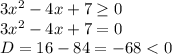
корней нет
делим обе части неравенства на 3х²−4х+7, 3х²−4х+7>0:
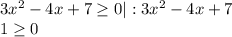
Неравенство выполняется, значит х ∈ R.
ответ: x ∈ (−∞; ∞).
3) x²−2x−3 > 0
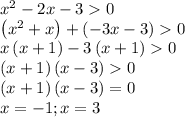
Определяем знаки на промежутках:
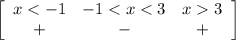
Интервалы x < −1 и x> 3 — удовлетворяют неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−∞; −1) ∪ (3; +∞).
Пошаговое объяснение:
1)6*6=4*9 , так как 36=36
2)5*7>8*3 , так как 35>24
3)6*9>3*6 , так как 54>18
4)8*1<3*3 , так как 8<9
5) 64:8=32:4 , так как 8=8
6)81:9>21:3 , так как 9>7
7)40:5>24:4 , так как 8>6
8)27:3=54:6 , так как 9=9