1. Найдите значение производной функции в точке x₀:
a) y=(3·x-2)⁷, x₀=3
y'=((3·x-2)⁷)'=7·(3·x-2)⁶·(3·x-2)'=7·(3·x-2)⁶·3=21·(3·x-2)⁶
y'(3)=21·(3·3-2)⁶=21·7⁶=21·117649=2470629
б) y=(4-5·x)⁷, x₀=1
y'=((4-5·x)⁷)'=7·(4-5·x)⁶·(4-5·x)'=7·(4-5·x)⁶·(-5)= -35·(4-5·x)⁶
y'(1)= -35·(4-5·1)⁶= -35·(-1)⁶= -35·1= -35
в) y=(2·x+3)⁵, x₀=2
y'=((2·x+3)⁵)'=5·(2·x+3)⁴·(2·x+3)'=5·(2·x+3)⁴·2=10·(2·x+3)⁴
y'(2)=10·(2·2+3)⁴=10·7⁴=10·2401=24010
г) y=(5-3·x)⁷, x₀=1
y'=((5-3·x)⁷)'=7·(5-3·x)⁶·(5-3·x)'=7·(5-3·x)⁶·(-3)= -21·(5-3·x)⁶
y'(1)= -21·(5-3·1)⁶= -21·2⁶= -21·64= -1344
2. Вычислить скорость изменения функции в точке x₀ (скорость изменения равносильно производная первого порядка):
a) y=(2x+1)⁵, x₀= -1
y'=((2·x+1)⁵)'=5·(2·x+1)⁴·(2·x+1)'=5·(2·x+1)⁴·2=10·(2·x+1)⁴
y'(-1)=10·(2·(-1)+1)⁴=10·(-1)⁴=10·1=10
б) 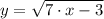 , x₀= 1
, x₀= 1


в)  , x₀= 2
, x₀= 2 
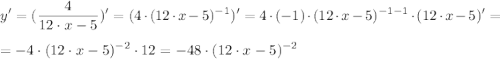

г) 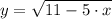 , x₀= -1
, x₀= -1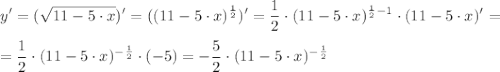
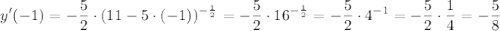
3. Найдите производные функций:
a) y=(x-1)·(x²+x+1) = x³-1
=1·(x²+x+1)+(x-1)·(2·x+1)= x²+x+1+2·x²+x-2·x-1 =3·x²
б) 

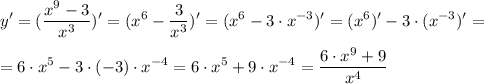
Даны вершины треугольника ABC: A(1; 3; 1), B(2; 5; 0), C(4; -1; 3).
Определяем векторы.
АВ (2-1=1; 5-3=2; 0-1=-1) = (1; 2; -1). Модуль (длина) = √(1+4+1) = √6.
ВС (4-2=2; -1-5=-6; 3-0=3) = (2; -6; 3). Модуль (длина) = √(4+36+9) = √49=7.
АС (4-1=3; -1-3=-4; 3-1=2) = (3; -4; 2). Модуль (длина) = √(9+16+4) = √29.
cos A = (AC x AB) / (|AC| * |AB|) = (3*1+(-4)*2+2*(-1)) / (√29*√6) =
= -7 / √174 ≈ -0,53067.
Угол А = 2,13019 радиан или 122,0506 градуса.
cos B = (BA x BC) / (|BA| * |BC|) = (-1*2+(-2)*(-6)+1*3) / (√6*7) =
= 13 / 7√6 ≈ 0,728175.
Угол В = 0,71029 радиан или 40,6964 градуса.
BA = (-1; -2; 1), BC = (2; -6; 3)
cos С = (СA x СB) / (|СA| * |СB|) = (-3*(-2)+4*6+(-2)*(-3)) / (√29*7) =
= 36 / 7√29 ≈ 0,955005.
Угол С = 0,30112 радиан или 17,2530 градуса.
СА = (-3; 4; -2),СВ = (-2; 6; -3).
Площадь S = (1/2)|AB| * |AC| * sin A = (1/2)* √6*√29*sin 122,0506° = 5,59017 кв.ед.
Площадь также равна половине модуля векторного произведения векторов АВ (1; 2; -1) на АС (3; -4; 2).
i j k | i j
1 2 -1 | 1 2
3 -4 2 | 3 -4 = 4i - 3j - 4k - 2j - 4i - 6k = (0i - 5j - 10k).
S = (1/2)√(0 + 25 + 100) = (1/2)√(125 = (5/2)√5 = 2.5*2,2361 ≈ 5,59017 кв.ед.