 и
и 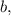 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
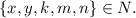
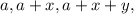 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и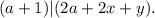
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;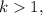 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.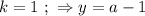 ;
;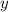 его значение
его значение 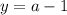 и будем искать такие комбинации
и будем искать такие комбинации 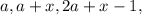 чтобы:
чтобы: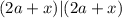 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 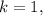
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и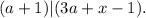
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;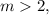 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.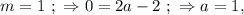 но это не подходит по условию.
но это не подходит по условию.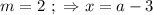 ;
; его значение
его значение 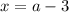 и будем искать такие комбинации
и будем искать такие комбинации 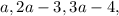 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 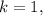
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 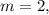
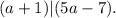
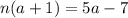 ;
;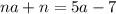 ;
; ;
;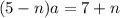 ;
;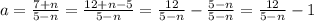 ;
;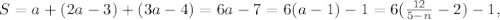
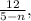 т.е. при
т.е. при 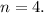
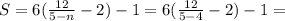
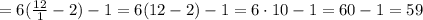 ;
;Даны четыре точки A (7,2,2) B (-5,7,-7) C (5,-3,1) D (2,3,7).
Составить уравнения:
1) плоскости ABC по точкам A (7,2,2) B (-5,7,-7) C (5,-3,1);
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA
= 0
Подставим данные и упростим выражение:
x - 7 y - 2 z - 2
(-5) - 7 7 - 2 (-7) - 2
5 - 7 (-3) - 2 1 - 2
= 0
x - 7 y - 2 z - 2
-12 5 -9
-2 -5 -1
= 0
x - 7 5·(-1)-(-9)·(-5) - y - 2 (-12)·(-1)-(-9)·(-2) + z - 2 (-12)·(-5)-5·(-2) = 0
(-50) x - 7 + 6 y - 2 + 70 z - 2 = 0
- 50x + 6y + 70z + 198 = 0 или, сократив на 2
25x - 3y - 35z - 99 = 0
2) прямой AB по точкам A (7,2,2) и B (-5,7,-7) ;
Вектор АВ найден в п. 1: (-1; 5; -9).
(x - 7)/(-1) = (y - 2)/5 = (z - 2)/(-9).
3) найти расстояние от точки D до плоскости ABC .
Нормальный вектор плоскости АВС (25; -3; -35) найден в п, 1.
Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D| /√(A² + B² + C²)
Подставим в формулу данные:
d = |25·2 + (-3)·3 + (-35)·7 + (-99)|/ √(25² + (-3)² + (-35)²) =
|50 - 9 - 245 - 99| /√(625 + 9 + 1225) =
= 303/ √1859 = 303√11/ 143 ≈ 7.0275336.
Пошаговое объяснение:
320 конечно но это не точно потому что не правильно дано задание