Пошаговое объяснение:
Зададим произвольное положительное рациональное число в виде несократимой дроби 
. Если разделить числитель дроби на знаменатель уголком, то в частном получим либо конечное, либо бесконечное периодическое ее десятичное разложение.
Конечное десятичное разложение подучится,если знаменатель q не имеет других простых делителей, кроме 2 и 5. В остальных случаях может быть только бесконечное десятичное разложение, которое является периодическим.
Например, число 6 раскладывается на произведение двух множителей 2 и 3: 6=2*3 . В этом разложении на множители есть число 3, которое отлично от 2 и 5, значит любая несократимая дробь со знаменателем 6 будет периодической десятичной дробью.
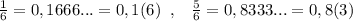
Аналогично,
2a^2+2a+4
Пошаговое объяснение:
1)a*a+a*(-3)=a^2-3a
2)a*a+a*4+1*a+1*4=a^2+5a+4
3)a^2-3a+a^2+5a+4=2a^2+2a+4