-10
Пошаговое объяснение:
Нам тут понадобится правило Лопиталя.
если 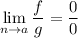 или
или 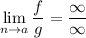 то
то 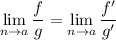
1
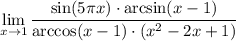
2 Вынесем -1 по формуле 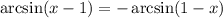
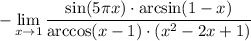
3 Запишем предел произведения дробей как произведение пределов
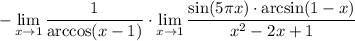
4 Подставим в первом пределе значение и посчитаем
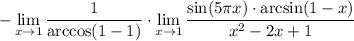
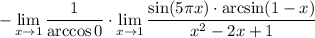
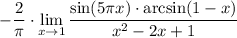
5 Cоберем квадрат в знаменателе 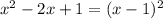
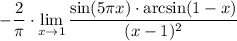
6 Получили предел вида  воспользуемся правилом Лопиталя
воспользуемся правилом Лопиталя
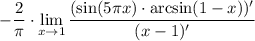
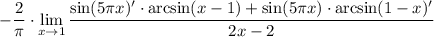
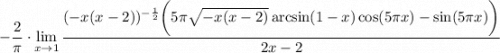
Тут я сразу вынес за скобки
7 Вынесем  (взял 2 в знаменателе) за предел и сократим
(взял 2 в знаменателе) за предел и сократим
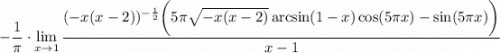
8 Распишем как произведение пределов
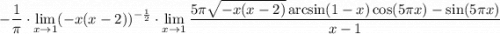
9 Посчитаем первый предел
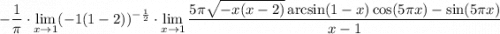
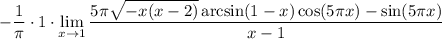
10 Распишем разность дробей в пределе
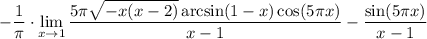
11 Распишем предел разности как разность пределов
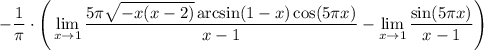
12 Распишем первый предел как произведение пределов и вынесем 5π
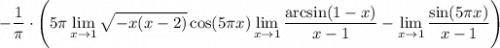
13 Посчитаем первый предел
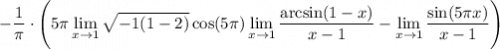
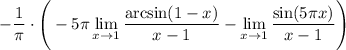
14 В первом пределе снова неопределённость  , снова Лопиталем
, снова Лопиталем
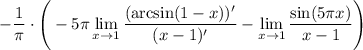
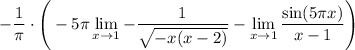
15 Теперь мы можем посчитать первый предел
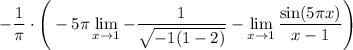
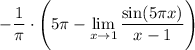
16 Снова используем правило Лопиталя, так как у нас неопределённость 
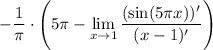
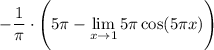
17 Выносим константу
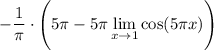
18 Посчитаем предел
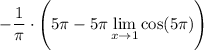
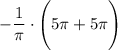
19 Досчитываем!
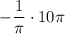

МЫ ПОЛУЧИЛИ ОТВЕТ
ответ: на расстоянии 450 м от поля оса догонит шмеля.
Пошаговое объяснение:
Пусть время, через которое оса догонит шмеля - х. ⇒
300+50*x=150*x
100x=300 |÷100
x=3 (мин.) ⇒
Расстояние, которое пролетит оса, чтобы догнать шмеля:
150*3=450 (м).