0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет 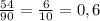
0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет 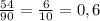
ответ :6823 + 6823 = 13646
Объяснение :Т. к сумма "О" должна давать в сумме двузначное число, "МНОГО" - это пятизначное число. получается что "О" - 5, 6, 7, 8, 9. затем, "О" на конце "МНОГО" и равняется "2хН", значит, "О" - четное число. Для "О" подходит 6 и 8. "М" - это 1.
тогда "Н" равно 2, 3 (если "О"=6) и 6, 7 (для "О"=8).
следует учесть из окончания, что 2х"Н"="О". тогда получается, что "Н"=3, "О"=6. 2х"Д" должно быть двузначным, чтобы "Н"=3.
2х"Д"=6, что допустимо только, если "Д"=3 или 8. 3 уже занято для "Н".