 ;
;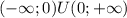 ;
;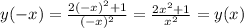 ;
;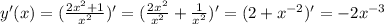 ;
;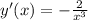 ;
;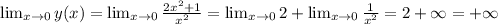 ;
; ;
; ;
;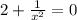 ;
;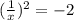 – что невозможно ни при каких действительных значениях аргумента;
– что невозможно ни при каких действительных значениях аргумента;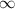 :
: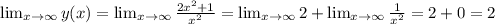 ;
;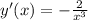 – положительна при отрицательных значениях аргумента и отрицательна при положительных х ;
– положительна при отрицательных значениях аргумента и отрицательна при положительных х ;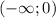 и убывает на
и убывает на 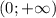 ;
;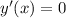 т.е.
т.е. 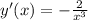 – не имеет решений, а значит, у функции нет экстремумов, т.е. конечных локальных минимумов или максимумов.
– не имеет решений, а значит, у функции нет экстремумов, т.е. конечных локальных минимумов или максимумов. ;
;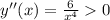 при любых значениях аргумента ;
при любых значениях аргумента ;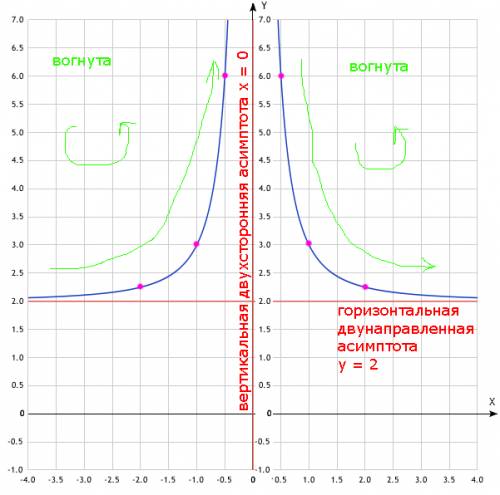
ответ: N = 10
Т.к. в N-ичной системе счисления присутствует число 7 (и, соответственно, цифра 7), то основание системы больше 7, т.е. N > 7.
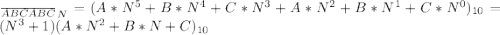
Так как 7 - простое число, то надо рассмотреть 2 случая: 1) 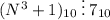 2)
2) 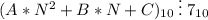 ∀ цифр A, B, C < N
∀ цифр A, B, C < N
1) 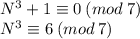
Представим N в виде x+7k, где k,x∈N∪{0}, x∈[0,6]. Подставим:
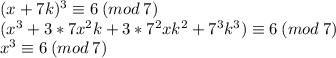
Последовательно подставляя все возможные значения x в полученное уравнение, получаем, что оно верно при x = 3, x = 5 и x = 6.
Получаем 3 серии решений: N = 3 + 7k, N = 5 + 7k, N = 6 + 7k, k∈N, откуда наименьшее N в данном случае, с учетом условия N > 7, равно 3 + 7 = 10
2) Так как утверждение должно быть верно для ∀ цифр A, B, C < N, то оно будет верно и для наборов (1, 0, 0) и (1, 0, 1).
Тогда: 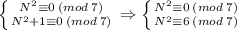
При этом 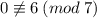 . Значит система сравнений не имеет решений. А значит не существует такого N, чтобы условие выполнялось
. Значит система сравнений не имеет решений. А значит не существует такого N, чтобы условие выполнялось
Значит и ответом будет N = 10
Если x=2,4 то (-4)+(1-3*2,4)
(-4)+(1-7,2)
(-4)+(-6,2)=-10.2