1170
Пошаговое объяснение:
Прежде всего нужно помнить признаки делимости на 5 и 9.
Число будет делиться на 5, когда последняя цифра этого числа равна 0 или 5.
Число будет делиться на 9, когда сумма цифр этого числа делится на 9.
Исходя из этого находим нужное число.
1155 - 1+1+5+5=12 - не подходит.
1150 - 1+1+5+0=7 - не подходит.
1160 - 1+1+6+0=8 - не подходит.
1145 - 1+1+4+5=11 - не подходит.
1165 - 1+1+6+5=13 - не подходит.
1140 - 1+1+4+0=6 - не подходит.
1170 - 1+1+7+0=9 - все признаки делимости подходят.
Следовательно, необходимое число найдено - это 1170.
Пошаговое объяснение:
1) область определения, непрерывность, четность/нечётность, периодичность функции.
2) асимптоты графика функции.
3) нули функции, интервалы знакопостоянства.
4) возрастание, убывание и экстремумы функции.
5) выпуклость, вогнутость и перегибы графика.
у= (х²-1)³
1) область определения, непрерывность, четность/нечётность, периодичность функции.
а) область определения, непрерывность
функция определена и непрерывна на всей числовой прямой
б) четность/нечётность
y(-x) = ((-x)² -1)³ = (x²-1)³ = y(x) - функция четная
в) периодичность
функция не тригонометрическая (периодичность определяется для тригонометрических функций
2) асимптоты графика функции
функция непрерывна - вертикальные асимптоты отсутствуют
уравнения наклонных асимптот обычно ищут в виде y = kx + b.
из определения асимптоты
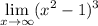
найдем коэффициент k
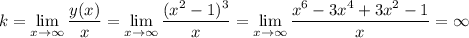
коэффициент k равен бесконечности, наклонных асимптот не существует
3) нули функции, интервалы знакопостоянства
a) нули функции
(x²-1)³ = 0 ⇒ x1 = 1; x2 = -1
б) интервалы знакопостоянства
(x²-1)³ > 0 ⇒ y(x) положительна при x ∈(-∞; -1) ∩(1; ∞)
(x²-1)³ < 0 ⇒ y(x) отрицательна при x ∈ (-1; 1)
4) возрастание, убывание и экстремумы функции
а) экстремумы функции
y' = 6x(x²-1)²
6x(x²-1)² = 0 ⇒ x1=0; x2=-1; x3=1 - это критические точки
смотрим значение функции в этих точках
f(0) = -1
f(-1) = 0
f(1) = 0
для определения какие это точки, используем достаточное условие экстремума функции одной переменной.
найдем вторую производную
y'' = 24x²·(x²-1)+6(x²-1)² = 30x⁴-36x²+6
смотрим знак второй производной в критических точках
y''(0) = 6 > 0 - точка x1 = 0 точка минимума функции
y''(-1) = 0 = 0 - точка x2 = -1 точка перегиба функции
y''(1) = 0 = 0 - точка x3 = 1 точка перегиба функции
б) возрастание, убывание
исходя из наличия критических точек мы имеем четыре интервала
(-∞ ;-1); (-1; 0); (0; 1); (1; +∞)
смотрим значение первой производной 6x(x²-1)² на этих интервалах
(-∞ ;-1) f'(x) < 0 - функция убывает
(-1; 0) f'(x) < 0 - функция убывает
(0; 1) f'(x) > 0 - функция возрастает
(1; +∞) f'(x) > 0 - функция возрастает
5) выпуклость, вогнутость и перегибы графика
а) точки перегиба нашли в п.4 - точки x2 = -1 и x3 = 1
б) интервалы выпуклости и вогнутости
у''(x) = 30x⁴-36x²+6
30x⁴-36x²+6 =0 ⇒ х1= -1; x2= 1; x3= -√5/5 ; x4 = √5/5
получим интервалы
(-∞; -1); (-1; -√5/5); (-√5/5; √5/5); (√5/5; 1); (1; ∞)
смотрим знак второй производной на этих участках
(-∞; -1) f''(x) > 0 - функция вогнута
(-1; -√5/5) f''(x) < 0 - функция выпукла
(-√5/5; √5/5) f''(x) > 0 - функция вогнута
(√5/5; 1) f''(x) < 0 - функция выпукла
(1; ∞) f''(x) > 0 - функция вогнута
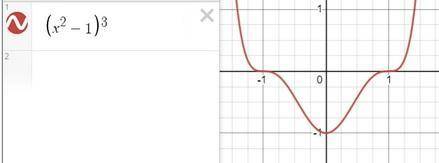
теперь можно построить график. можно добавить какие-нибудь точки дополнительные. а можно и по уже найденным точкам схематично построить график
я построю при программы
Составим уравнение:
ответ: 3/2