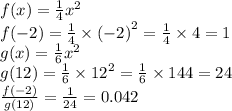
Решите уравнениеx^-2x+√6-x=√6-x+35
ответ или решение1
Давайте начнем решение уравнения x^2 - 2x + √(6 - x) = √(6 - x) + 35 с нахождения его области определения.
Итак, выражение под знаком квадратного корня не может принимать значение меньше нуля.
6 - x ≥ 0;
x ≤ 6.
Итак, получаем уравнение:
x^2 - 2x + √(6 - x) - √(6 - x) - 35 = 0;
x^2 - 2x - 35 = 0;
Решаем квадратное уравнение:
D = b^2 - 4ac = (-2)^2 - 4 * 1 * (-35) = 4 + 140 = 144;
Ищем корни уравнения:
x1 = (-(-2) + √144)/2 * 1 = (2 + 12)/2 = 14/2 = 7;
x2 = (-(-2) - √144)/2 * 1 = (2 - 12)/2 = -10/2 = -5 корень не принадлежит ОДЗ.
ответ: 7.
7 см
Пошаговое объяснение:
Если прямая перпендикулярна к плоскости, то она перпендикулярна к каждой прямой в этой плоскости, поэтому все треугольники AOK, BOK, COK и DOK с прямым углом.
К тому же они все одинаковы, так как имеют общий катет OK, диагонали квадрата также одинаковы и делятся в точке пересечения пополам OA=OB=OC=OD.
Значит, KA=KB=KC=KD, поэтому необходимо рассчитать только одно расстояние.
Проведём расчёты в треугольнике AOK. Если сторона квадрата равна 9 см, то диагональ квадрата равна 92√ см. AO равно половине диагонали.
По теореме Пифагора рассчитаем KA:
KA=(3)2+(92√2)2−−−−−−−−−−−−−−√≈ 7 см.