6. Масса ящика с помидорами равна 20 кг
а с морковью на 4 кг больше. Сколько
Килограммов составляет масса Ящика с
морковью?

Question

Математика: 6. Масса ящика с помидорами равна 20 кг а с морковью на 4 кг больше. Сколько Килограммов составляет масса Ящика с морковью?​

zilga1 · Accepted Answer

Из формулы классического определения вероятности, найдем искомую вероятность :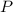

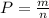$P=\frac{m}{n}$ -------(1)

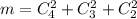$m=C^{2}_{4}+C^{2}_{3}+C^{2}_{2}$ ------(2)

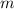- число благоприятных исходов

При этом

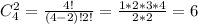
$C^{2}_{4}=\frac{4!}{(4-2)!2!}=\frac{1*2*3*4}{2*2}=6$

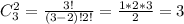
$C^{2}_{3}=\frac{3!}{(3-2)!2!}=\frac{1*2*3}{2}=3$

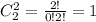
$C^{2}_{2}=\frac{2!}{0!2!}=1$

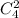$C^{2}_{4}$ - число сочетаний из 4-х синих шаров по 2 синих шара

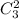$C^{2}_{3}$ - число сочетаний из 3-х красных по 2 красных

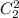$C^{2}_{2}$ - число сочетаний из 2-х зеленых по 2 зеленных

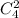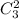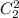Подставим в (2) вместо $C^{2}_{4}$ , $C^{2}_{3}$ и $C^{2}_{2}$ их значения, найдем:

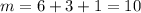
m=6+3+1=10

В свою очередь число всех исходов 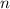равно числу сочетаний из всех 9 шаров по 2 в каждом, т.е.

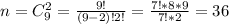
$n=C^{2}_{9}=\frac{9!}{(9-2)!2!}=\frac{7!*8*9}{7!*2}=36$

Подставляя в (1) вместо 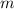и 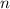их найденные значения, найдем искомую вероятность:

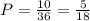
$P=\frac{10}{36}=\frac{5}{18}$

6. Масса ящика с помидорами равна 20 кга с морковью на 4 кг больше. СколькоКилограммов составляет масса Ящика сморковью?​