Дана трапеция АВСД. Основание АД=22. ДМ - биссектриса, точка М - точка пересечения биссектрисы и боковой стороны АВ, АМ=10, МВ=5
Проведём прямую МК параллельную АД, /КМД=/МДА - накрест лежащие. /КДМ=/МДА, т.к. ДМ - биссектриса, следовательно, /КДМ=/КМД, т.е. треугольник МКД равнобедренный (по признаку), имеем МК=КД, но КД=АМ=10, то МК=10
МН - высота треугольника АМД, в нём АН=(22-10):2=6 (по свойству оснований равнобокой трапеции). По Т.Пифагора находим МН как катет прямоугольного треугольника АМН с гипотенузой 10 и другим катетом 6, МН=8.ВО перпендикуляр к МК. Треугольники АМН и МВО подобны с к=2, т.е. ВО=8:2=4, МО=6:2=3.
Имеем: высота трапеции равна 8+4=12, второе основание ВС=10-3·2=4 (по свойству оснований равнобокой трапеции)
Площадь трапеции равна полусумме оснований умноженная на высоту, т.е. S=(4+22):2·12=156
Відповідь:
1. Г)
2. Б)
3. В)
4. А)
5. В)
6. А)
7. На фото.
8. Розв'язуємо методом додавання.
Друге рівняння домножаємо на 3.
Відповідь: 2; -3.
На фото знизу.
9.
Нехай х - власна швидкість теплохода,
у - швидкість течії.
Значить складаємо рівняння:
(х + у) - швидкість за течією,
(х - у) - швидкість проти течії.
Значить складаємо систему:
{4(х + y) +5(x - y) = 214
{6(x+y) + 3(x-y)=222
{9x=214 + y
{9x=222-3y
214 + y=222-3y
у+3у=222-214
4y=8
у=8:4
y=2
9x=214 + 2
9x=216
х=216:9
x=24 (км/год)
Тоді, 24-2=22 (км/год).
(Від власної швидкості теплохода віднімаємо швидкість течії).
Відповідь: швидкість теплохода проти течії 22 км/год.

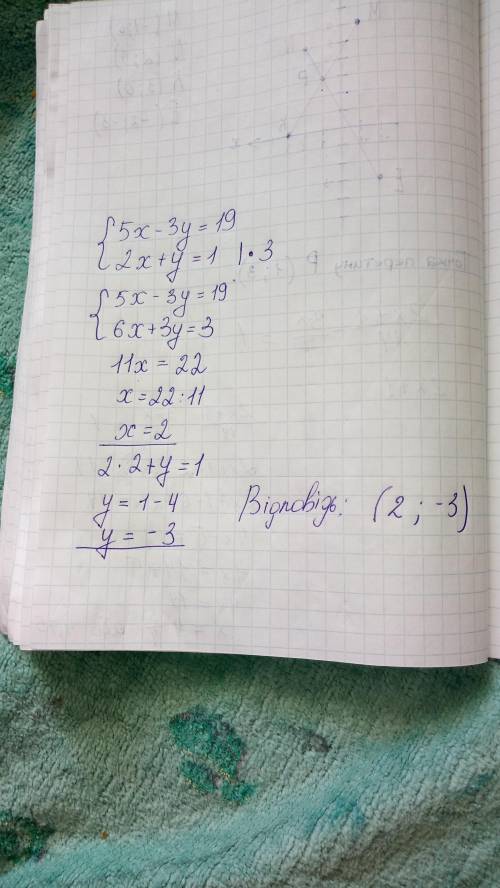
Бан бан бан бан