ответ: будет ровно пять
Пошаговое объяснение:
Пошаговое объяснение:
Предположим, что утверждение задачи не верно. Обозначим сумму цифр числа n через S(n). Среди любых 39 последовательных натуральных чисел обязательно найдётся не менее трёх делящихся на 10; пусть a минимальное из них. При этом получаем, что среди данных 39 чисел также есть и a + 1,..., a + 29. Поскольку a делится на 10, то S(a + 1) = S(a) + 1, S(a + 2) = S(a) + 2,..., S(a + 9) = S(a) + 9. Поэтому среди чисел a, a + 1,..., a + 9 не встречается число, сумма цифр которого делится на 11, только если S(a) $ \equiv$ 1 mod 11. При этом если a + 10 не делится на 100, то S(a + 10) = S(a) + 1, а значит, среди чисел a + 10, a + 11,..., a + 19 найдётся такое, что сумма его цифр делится на 11. Получили противоречие. Осталось рассмотреть случай, когда a + 10 делится на 100. Но тогда заметим, что S(a + 20) = S(a + 10) + 1, а значит, аналогично первому случаю среди чисел a + 10, a + 11,..., a + 29 найдётся число, сумма цифр которого делится на 11. Опять получили противоречие, значит, утверждение задачи верно.
5
Пошаговое объяснение:
ну, перед нами п/у треугольник
перед нами имеется угол в 60 градусов, известна гипотенуза, и нужно найти прилежащий катет
для этого как раз-таки есть косинус
cos B =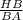
а cos 60°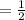
следовательно по правилу пропорции
2HB = BA
HB =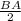 =5
=5
или также можно сказать, что другой угол равен 30°, а как мы знаем, катет, лежащий против угла в 30° равен половине гипотенузы, откуда
HB =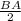 =5
=5