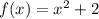Даны координаты точки. Определи, на которой координатной оси находится данная точка.

Точка B(0;−3) находится на оси

👇

Увидеть ответ

Ответ:

kivrosa

13.07.2022

На оси ОХ

Поставь корону

4,5(24 оценок)

Открыть все ответы

Ответ:

Kotik77789

13.07.2022

Пусть функция f(x)=x^2+2

определена на множестве E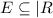 $E\subseteq |R$
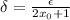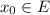Пусть $\delta=\frac{\epsilon}{2x_0+1}$ где $x_0 \in E$ .
Понятно, что для любого

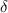на области $\delta$ от x_0

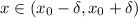(то есть: $x \in 
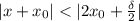(x_0-\delta,x_0+\delta)$ ) выполняется $|x+x_0|<|2x_0+ \frac{\delta}{2}|$ .
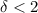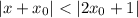Следовательно, для $\delta<2$ , выполняется |x+x_0|<|2x_0+1|

.

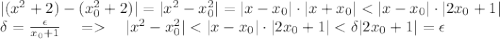
$|(x^2+2)-(x_0^2+2)|=|x^2-x_0^2|=|x-x_0|\cdot|x+x_0| < |x-x_0|\cdot|2x_0+1| \\
\delta= \frac{\epsilon}{x_0+1} \ \ \ = \ \ \ |x^2-x_0^2|< |x-x_0|\cdot|2x_0+1|<\delta|2x_0+1|=\epsilon$

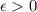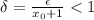Получили, что для любого $\epsilon 0$ есть $\delta=\frac{\epsilon}{x_0+1}<1$ , на области которой выполняется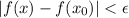 $|f(x)-f(x_0)|<\epsilon$
(Проще говоря:
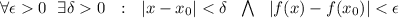$\forall
 \epsilon0 \ \ \exists\delta0 \ \ : \ \ |x-x_0|<\delta \ \ 
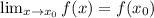\bigwedge \ \ |f(x)-f(x_0)|<\epsilon$ ). Следовательно - $\lim_{x 
\to x_0} f(x)=f(x_0)$ .
Что и требовалось доказать.
Для x_0=-1

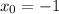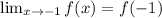нужно отдельно доказать предел $\lim_{x \to -1} f(x)=f(-1)$ .

Теперь в чём проблема самого вопроса: мы только что доказали непрерывность функции на любом подмножестве

. Но! Множество натуральных чисел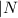

тоже подмножество

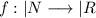, значит $f:|N \longrightarrow |R$ тоже непрерывна, получается - доказали что

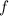непрерывна на области определения? Известно, что 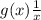$g(x) \frac{1}{x}$ тоже непрерывна на области определения, но

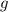, понятное дело, не определена на

!
Потому вопрос, ИМХО, поставлен не верно (претензия не к тебе, а скорее к преподавателям твоим). Правильно задать вопрос указывая то множесто точек, которое интересует: к примеру "непрерывна на

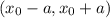" или, "непрерывна на отрезке (x_0-a,x_0+a)

"...
Тем более, что есть понятие "равномерная непрерывность" - свойство области, а не так, как "непрерывность" - свойство точки. Отсюда и непонимание.
А то получается: спрашивают об области, а проверяют точку.
Будут вопросы - пиши.

P.S. Исправил ошибки в наборе символов. Текста много :)

4,7(52 оценок)

Ответ:

arslanmax

13.07.2022

21 человек

Пошаговое объяснение:

Петя на карусели

впереди ---? дет. но берет 1/4

позади ? дет, но берет 4/5

всего ? но равно сумме 1/4 впереди и 4/5 позади

Решение.

1. Л о г и ч е с к о е

Так как Петя катается на карусели, то число детей впереди него равно числу детей позади него (все дети расположены по кругу).

Число детей без Пети делится на 4 и 5. И оно является наименьшим общим кратным 4 и 5, так как отличается от общего числа детей только на одного человека: Петю.

НОК (4; 5) = 20

20 + 1 = 21 (чел.) всего

ответ: 21 человек

2. А р и ф м е т и ч е с к о е.

1 - число детей без Пети

1/4 + 4/5 = 21/20 всего человек в частях.

21/20 - 1 = 21/20 - 20/20 = 1/20 часть, которую составляет Петя по отношению к остальным детям

1 : (1/20) = 20 (чел.) дети без Пети

20 + 1 = 21 (чел.) всего детей на карусели

ответ: 21 человек

3. А л г е б р а и ч е с к о е

Х чел. число детей без Пети