Пошаговое объяснение:
1. нужно взять два прямоугольных треугольника таких, чтобы один из катетов был равен половине гипотенузы, например а = 0,5с (с - гипотенуза)
сложить эти треугольники катетами b "друг к дружке". получим равносторонний треугольник со сторонами равными с
и площадью S = (c²√3)/4
2. извините, не соображу наверное опять же прямоугольный треугольник, только складывать надо гипотенузами друг к другу
3. вероятностью наступления события в некотором испытании называют отношение Р(А) = m/n
m - общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий,
n - количество элементарных исходов, благоприятствующих событию A
теперь, что у нас.
в результате броска кубика может появиться n = 6 элементарных равновозможных исходов, образующих полную группу - 6 сторон и может выпасть одна из них с одинаковой вероятностью
а событию выпадения любой стороны благоприятствует единственный исход (выпадение этой стороны).
В₁ - выпадение 1, В₂ - двойки , и т.д.
и вот что у нас получается
Р(В₁) = Р(В₂) = Р(В₆) = 1/6
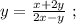
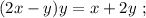
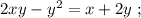
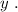Выражая из него 
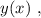мы получили бы стандартное выражение в виде корней параметрического квадратного уравнения, которых за исключением одной точки всегда 2, в том случае, если они конечно вообще есть. Таким образом, если бы мы использовали функцию 
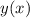относительно 
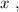для отображения того же множества точек, что и исходное уравнение, то такая функция, во-первых, не была бы однозначной, а во-вторых была бы определана не для всех 
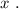Вывод: для дифференцирования такого уравнения наиболее удобно использовать именно однозначную обратную функцию 
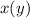относительно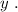 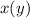относительно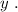 
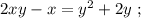
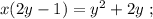
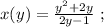
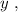используя общее правило,
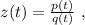то: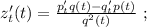 
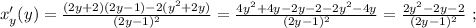
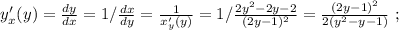
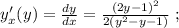
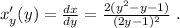
1)3<(x+4)<5
-1<x<1
2)-1<x-2/3<5
-1/3<x<17/5
-1/3<x<5(2/3)