Если одна из цифр 0, то она не может быть первой. 100, 110, 101 - всего 3*9 = 27 вариантов, по 3 на каждую цифру 1-9. Если 0 нет, то первой может быть любая из двух цифр. 112, 121, 211, 122, 212, 221 - всего 6*9*8 = 432 варианта. Вместо 1 может быть любая из цифр от 1 до 9, вместо 2 - любая из остальных 8 цифр. Всего 8*9 = 72 варианта. И для каждой пары цифр возможно по 6 перестановок. Итак, всего получается 432 + 27 = 459 вариантов, но такого ответа нет. Интересно, где я ошибся? Или ошиблись авторы задачи?
При умножении дроби на натуральное число, мы должны ее числитель умножить на это число, а знаменатель оставить без изменения.
Умножаем только 7 в числителе на число 3.
Чтобы умножить смешанную дробь на натуральное число, мы должны умножить и целую часть и числитель дроби на это число.
Умножаем и 1 в целой части и 2 в числителе на число 3.
При умножении простой дроби на простую дробь, надо: 1) перемножить числители этих дробей и результат записать в числитель 2) перемножить их знаменатели и результат записать в знаменатель
Перемножаем 2 и 3 в числителе, а 5 и 4 в знаменателе.
Для умножения смешанных чисел, надо записать их в виде неправильных дробей, а затем воспользоваться правилом умножения простых дробей.
Преобразуем смешанные числа в неправильные дроби, а затем перемножаем их.
Если ты имеешь в виду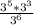
Пошаговое объяснение:
ответ будет: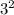 если решить и это будет 9
если решить и это будет 9
Мне кажется разберешься как записать