Теорема (свойство медианы равнобедренного треугольника). В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
Доказательство. Пусть ABC – данный равнобедренный треугольник с основанием AB и CD – медиана, проведённая к основанию (рис. 53).
Треугольники CAD и CBD равны по первому признаку равенства треугольников. (У них стороны AC и BC равны, потому что треугольник ABC равнобедренный. Углы CAD и CBD равны как углы при основании равнобедренного треугольника. Сторона AD и BD равны, потому что D – середина отрезка AB.)
Из равенства треугольников следует равенство углов: угол ACD = углу BCD, угол ADC = углу BDC. Так как углы ACD и BCD равны, то CD – биссектриса. Так как углы ADC и BDC смежные и равны, то они прямые, поэтому CD – высота треугольника.
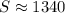 см².
см².
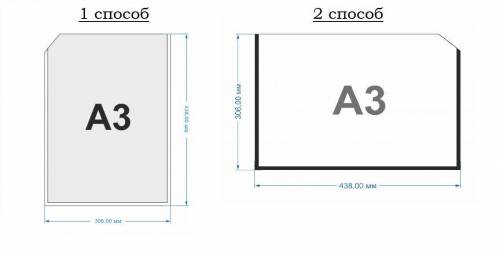
вертикальный лист формата а3).
 (длина)
(длина) 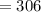 мм
мм 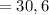 см.
см.
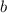 (ширина)
(ширина) 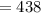 мм
мм 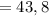 см.
см.
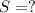 см².
см².
------------------------------------------------
Лист формата а3 имеет прямоугольную форму, поэтому его площадь находится по формуле площади прямоугольника: 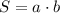 .
.
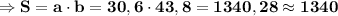 см².
см².
=======================================================
горизонтальный лист формата а3).
 (длина)
(длина) 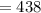 мм
мм 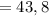 см.
см.
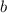 (ширина)
(ширина) 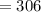 мм
мм 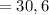 см.
см.
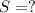 см².
см².
------------------------------------------------
Лист формата а3 имеет прямоугольную форму, поэтому его площадь находится по формуле площади прямоугольника: 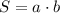 .
.
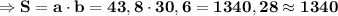 см².
см².
=======================================================
ответ:х×(х+3)=х+60
2х+3х=х+60
5х=х+60
5х-х=60
4х=60
х=60/4
х=15 сторинок