Пусть а - сумма вклада на конец первого года, х - количество процентов, выраженные десятичной дробью, на которое увеличивается вклад в конце каждого года.
Тогда а+ах - сумма вклада на конец второго года.
ах - это та величина, на которую увеличился вклад на конец второго года хранения. По условию она равна 2500 рублей.
ах=2500
а+ах +х(а+ах)=а(1+х)+ах(1+х)=(а+ах)(1+х)=а(1+х)(1+х)=а(1+х)² - сумма вклада на конец третьего года хранения.
а(1+х)²+ха(1+х)² - сумма вклада на конец четвертого года хранения
ха(1+х)² - это величина, на которую увеличился вклад на конец четвертого года хранения. По условию она равна 3600 рублей.
ха(1+х)² =3600
Составим систему.
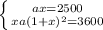
Из первого уравнения выразим а и подставим его во второе уравнение.

Второй корень посторонний, т.к. меньше нуля.
х=0,2.
Значит ежегодно вклад увеличивается на 20%.
Найдем а:
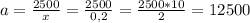
Сумма вклада на конец четвертого года:
а(1+х)²+ха(1+х)²=(а+ах)(1+х)²=а(1+х)(1+х)²=а(1+х)³
На конец пятого года сумма вклада будет составлять:
а(1+х)³+ха(1+х)³, т.е. на конец пятого года вклад увеличится на ха(1+х)³.
Подставим найденные х и а и вычислим эту величину.

ответ: за пятый год вклад увеличится на 4320 рублей.
∫(-х² - х +2)dx = (-x³/3)-(x²/2) + 2x.
Найдём границы фигуры по оси х.
Приравняем -x² - 2x - 1 = -x - 3,
-x² - x + 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-1)^2-4*(-1)*2=1-4*(-1)*2=1-(-4)*2=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√9-(-1))/(2*(-1))=(3-(-1))/(2*(-1))=(3+1)/(2*(-1))=4/(2*(-1))=4/(-2)=-4/2=-2;x_2=(-√9-(-1))/(2*(-1))=(-3-(-1))/(2*(-1))=(-3+1)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1.
Получили 2 точки х = -2 и х = 1.
Подставляем пределы в интеграл:
(-x³/3)-(x²/2) + 2x|(-2;1)= (-1/3)-(1/2)+2 - (8/3)-(4/2)-4) =
(7/6)-(-20/6) = 27/6 = 9/2 = 4,5.