Десятичная дробь - это разновидность дроби , которая представляет собой представления в виде где ; либо,- десятичная запятая , служащая разделителем между целой и дробной частью числа ,- десятичные числа
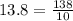
- говорится 138 десятых
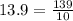
- говорится 139 десятых
Если эти числа записать 13,80 и 13,90 , то между числами стоят 13,81 , 13,82 , 13,83 , 13,84 ,13,85 , 13,86 , 13,87 ,13,88 , 13,89 и 13,90
1. у=2х+10
D(f)=R
E(f)=R
Нули функции;
2х+10=0
2х=-10
х=-10/2
х=-5
Промежутки возрастания (-∞;∞)
Не периодическая.
f(-x)=2(-x)+10=-2x+10≠f(x)≠-f(x), значит Ни четная, ни нечётная.
Промежутки знакопостоянства:
у>0 на хє(-5;∞)
y<0 на хє(-∞;-5)
Экстремумов нет, т.к нет таких точек, что две соседние находились ниже или выше такой точки.
2. у=-4/х
D(f)=(-∞;0)U(0;∞)
E(f)=(-∞;0)U(0;∞)
Нули функции:
-4/х=0
ОДЗ: х≠0
Нет нулей.
Промежутки возрастания: хє(-∞;0)U(0;∞)
не периодическая.
f(-x)=-4/(-x)=4/x=-(-4/x)=-f(x), нечётная.
Промежутки знакопостоянства:
у>0 на хє(-∞;0)
y<0 на хє(0;∞)
Экстремумов нет, т.к нет таких точек, что две соседние находились ниже или выше такой точки.
-1
Пошаговое объяснение:
Можно было немного упростить себе жизнь: выразить все факториалы через n! и сократить на него. Для начала упростим дробь:
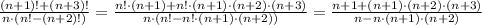
Можем раскрыть каждое произведение и запутаться. А можем просто вынести из каждой скобки общий множитель n . Тогда дробь примет вид:
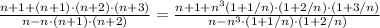
Вернемся к пределу и вспомним, что предел отношения полиномов
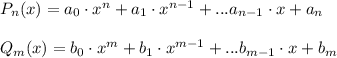
При переменной, стремящейся к бесконечности равен:
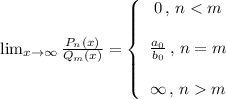
Тогда, для этой задачи такой предел равен отношению коэффициентов перед n³ (слагаемые вида 1/n стремятся к 0, а значит сама скобка стремится к 1)
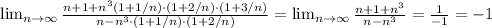
13,81; 13,82; 13,83; 13,84; 13,85; 13,86; 13,87; 13,88; 13,89.
Также могут быть варианты, например, 13,8563. И так до бесконечности.