К сумме чисел 1,05 и −11\20(одна целая одна двадцатая) прибавь число, обратное числу 11\6(одна целая одна шестая).

Составь выражение и найди его значение.

👇

Увидеть ответ

Ответ:

alinabilalova161

26.03.2023

1.05 = 1 \: \frac{1}{20}

1 \: \frac{1}{20} - 1 \: \frac{1}{20} = 0

1 \: \frac{1}{24} = \frac{25}{24}

Чтобы найти обратное число к данному, нужно " перевернуть " дробь верх ногами

0 + \frac{24}{25} = \frac{24}{25} = 0.96

ответ: 24/25 или 0.96

Пошаговое объяснение:

4,8(3 оценок)

Открыть все ответы

Ответ:

RMDEL

26.03.2023

Ю́жная Аме́рика (исп. América del Sur, Sudamérica, Suramérica, порт. América do Sul, англ. South America, нидерл. Zuid-Amerika,фр. Amérique du Sud, гуар. Ñembyamérika, кечуа Urin Awya Yala, Urin Amerika) — южный континент в Америке, расположенный в основном в Западном и Южном полушариях планеты Земля, тем не менее, частично континент располагается и в Северном полушарии. Омывается на западе Тихим океаном, на востоке — Атлантическим, с севера ограничивается Северной Америкой, граница между Америками проходит по Панамскому перешейку и Карибскому морю.В состав Южной Америки также входят различные острова, большинство из которых принадлежит странам континента. Острова в бассейне Карибского моря относятся к Северной Америке. Страны Южной Америки, которые граничат с Карибским морем — включая Колумбию, Венесуэлу, Гайану, Суринам и Французскую Гвиану — известны как Карибская Южная Америка.Слово «Америка» в названии этого континента впервые применил Мартин Вальдземюллер, нанеся на свою карту латинский вариант имени Америго Веспуччи, который, в свою очередь, впервые предположил, что открытые Христофором Колумбом земли не имеют отношения к Индии, а являются Новым Светом, прежде европейцам неизвестным.

4,7(53 оценок)

Ответ:

waleruwka

26.03.2023

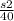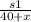Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была $\frac{s2}{40}$ , а после встречи $\frac{s1}{40+x}$ . Скорость второго пешехода до встречи и после встречи была одинаковой, значит $\frac{s1}{40+x}=\frac{s2}{40}$ , откуда $\frac{s1}{s2}=\frac{40+x}{40}$ . 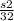У первого пешехода до встречи была скорость $\frac{s1}{40}$ , а после встречи $\frac{s2}{32}$ , скорость первого пешехода до встречи и после встречи была одинаковой, значит 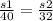$\frac{s1}{40}=\frac{s2}{32}$ , откуда 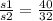$\frac{s1}{s2}=\frac{40}{32}$ . По условию задачи составим уравнение $\frac{40+x}{40}=\frac{40}{32}$ .