Пусть x и y - длины катетов, z - длина гипотенузы.
По теореме Пифагора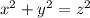 
Тройка сторон прямоугольного треугольника (x, y, z), где x нечётное, может быть представлена в виде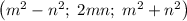 
.
Но эта тройка будет примитивной, т.е. состоять из взаимно простых чисел, а число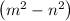 
должно быть нечётным. Нужно найти такие нечётные числа 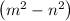, которые являются делителями числа 18.
Таких чисел всего два - 3 и 9.
Варианты с египетским треугольником понятны: (3, 4, 5) и производные - (6, 8, 10); (9, 12, 15); (12, 16, 20); (15, 20, 25); (18, 24, 30) и т.д. (умножаем числа тройки на одно и то же число). В случае (18, 24, 30) периметр треугольника будет равен 72.
Но не так сложно найти такие m и n, что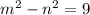 
. Очевидно, что m = 5, n = 4. Отсюда находим примитивную тройку (9, 40, 41).
В нашем случае тройка должна начинаться числом 18 (т.к. периметр должен быть максимальным, то есть известная сторона - это наименьший катет), значит все числа тройки умножаем на 2 и получаем (18, 80, 82).
Периметр такого треугольника равен 18+80+82 = 180.
16 2/3 км/час.
Пошаговое объяснение:
Пусть собственная скорость катера х км/час, тогда его скорость по течению х+(8/3) км/час, скорость против течения х-(8/3) км/час. Составим уравнение:
3(х+(8/3))=66
х+(8/3)=22
х=22 - 8/3
х=58/3=19 1/3
Собственная скорость катера 19 1/3 км/час.
Скорость катера против течения 19 1/3 - 8/3 = 50/3 = 16 2/3 км/час.
Второй
66:3=22 (км/час) скорость катера по течению
22 - 2 2/3 = 19 1/3 (км/час) собственная скорость катера
19 1/3 - 2 2/3 = 16 2/3 (км/час) скорость катера против течения.