Вроде так:Dans mon enfance je voulaius etre le policier. Je voulais aider des gens et savoir tous les lois. Mais cette profession est tres difficile et dangereuse. Tous les jours je dois laver tot, attraper des criminaux... Mais je pouvais aider des gens et garder le loi! Et maintenant je veux etre le policier. J'espere que je pourrai accomplir mon reve! Перевод: В моем детстве я хотел стать полицейским. Я хотел людям и знать все законы. Но эта профессия очень трудная и опасная. Каждый день я должен вставать рано, ловить преступниковНо я смог бы людям и охранять закон! И сейчас я хочу быть полицейским. Я надеюсь, что я смогу выполнить мою мечту!
Для решения данной задачи нам понадобится знание о свойствах параллелограмма и алгебраических операциях над векторами.
Свойства параллелограмма:
1. Противоположные стороны параллелограмма равны.
2. Противоположные углы параллелограмма равны.
3. Диагонали параллелограмма делятся пополам.
Обозначим параллелограмм как ABCD, где A и C - противоположные вершины, а B и D - противоположные вершины.
Задача состоит в выражении векторов tm и st через векторы a и b. Для этого распишем векторы tm и st через векторы AB и BC (потому что параллелограмм ABCD):
1. Вектор tm:
Вектор tm можно выразить как вектор AB, так как AB - это одна из сторон параллелограмма.
Запишем:
tm = AB
2. Вектор st:
Чтобы выразить вектор st через векторы a и b, воспользуемся определением векторного произведения векторов. Векторное произведение векторов a и b обозначается как a x b.
Запишем:
st = a x b
Таким образом, векторы tm и st выражены через векторы a и b следующим образом:
tm = AB
st = a x b
Объяснение:
- Вектор tm равен вектору AB по свойству параллелограмма.
- Вектор st выражен через векторное произведение векторов a и b, потому что так задано в условии задачи.
Шаги решения:
1. Записываем выражение для вектора tm: tm = AB
2. Записываем выражение для вектора st: st = a x b
Пошаговое объяснение:
Підставляємо в друге рівняння з системи
2(4+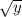 )+3
)+3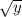 =18
=18
Розв'язуємо рівняння
8+2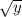 +3
+3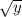 =18
=18
5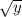 =10
=10
Підставляємо це значення в перше рівняння системи