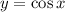
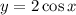
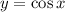 . Отличается лишь область значений.
. Отличается лишь область значений.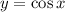 область значений следующая:
область значений следующая:![E(\cos x)=[-1,1]](/tpl/images/0579/2389/1dd9b.png)

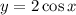 :
: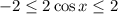
![E(y)=[-2,2]](/tpl/images/0579/2389/4690c.png)
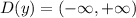 - область определения
- область определения 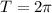 - период функции (все тригонометрические функции периодичны) .
- период функции (все тригонометрические функции периодичны) .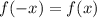
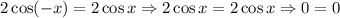 - тождество.
- тождество.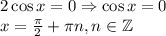
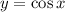 достигает экстремумы на концах отрезка области значения, то и
достигает экстремумы на концах отрезка области значения, то и 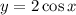 достигает экстремумы на концах отрезка:
достигает экстремумы на концах отрезка:![[-2,2]](/tpl/images/0579/2389/82b6c.png)
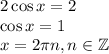 - максимумы.
- максимумы.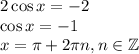 - минимумы.
- минимумы. и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на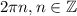
 и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на 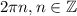
![[\pi,2\pi]](/tpl/images/0579/2389/a222e.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 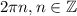
![[0,\pi]](/tpl/images/0579/2389/2a07b.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 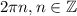

sinx+cosx=t
Возводим в квадрат
sin²x+2sinxcosx+cos²x=t²
Так как sin²x+cos²x=1, 2sinxcosx=sin2x, то 1+sin2x=t²⇒sin2x=t²-1
Уравнение примет вид:
t=1-(t²-1)
t²+t-2=0
D=1+8=9
t=(-1-3)/2=-2 или t=(-1+3)/2=1
sinx+cosx=-2 уравнение не имеет корней. Так как наименьшее значение синуса и косинуса равно -1, а это значение одновременно и синус и косинус принимать не могут.
sinx+cosx=1
Решаем методом введения вс угла.
Делим уравнение на √2:
(1/√2)sinx+(1/√2)cosx=1/√2.
sin(x+(π/4))=1/√2.
x+(π/4)=(π/4)+2πk, k ∈Z или x+(π/4)=(3π/4)+2πn, n∈Z;
x=2πk, k∈Z или x=(π/2)+2πn, n∈Z.
ответ.2πk; (π/2)+2πn; k,n∈Z.