да
Пошаговое объяснение:
умножение и деление выполняется первыми, затем +- по порядку. так как уравнение не содержит скобки ()
должно выйти 30
Бесконечно длинных арифметических прогрессий состоящих только из степеней не существует. Докажем это. Пусть есть прогрессия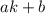 
, где 
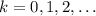Пусть НОД 
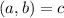. Перепишем нашу прогрессию так:
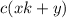, где 
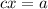и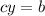 
. В этом случае числа 
и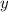 
взаимно просты. По теореме Дирихле, в арифметической прогрессии, у которой разность и первый член взаимно просты, есть бесконечно много простых чисел. Если число 
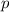простое и 
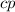- это степень, тогда очевидно 
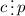. Получается, что число 
делится на бесконечное кол-во простых чисел, а значит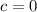 
, и наша последовательность - не прогрессия.
Поэтому, скорее всего имеются в виду прогрессии любой наперед заданной длины. Они как раз существуют. Покажем, как построить такую прогрессию. Будем пытаться сделать прогрессию длины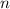 
такого вида:
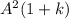
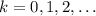
т. е. некоторое число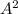 
умножается на натуральный ряд:
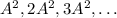
Видно, что в этом случае первый член являтся второй степенью. Потребуем также, чтобы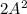 
было 3-ей степенью, 
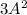было 5-ой степенью, и так далее: 
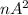- степень с показателем 
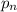- n-ым простым числом.
Представим число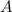 
в виде
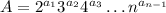
Возьмем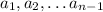 
такие, что
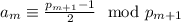
и
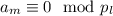если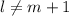 
(естественно 
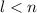). Доказательство того, что такие числа 
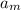существуют сразу следует из китайской теоремы об остатках.
В этом случае для любого натурального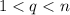 
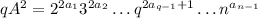
Из построения 
мы знаем, что все 
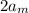кроме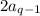 
делятся на 
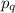. Но
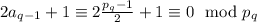
Таким образом доказано, что все показатели степеней в разложении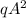 
делятся на 
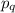а это означает, что
Указанным выше можно построить сколь угодно длинную арифметическую прогрессию, состоящую только из степеней.
ответ: 36:4+7х3=9+21=30