(см. объяснение)
Пошаговое объяснение:
Приведу несколько идей к решению:
1:
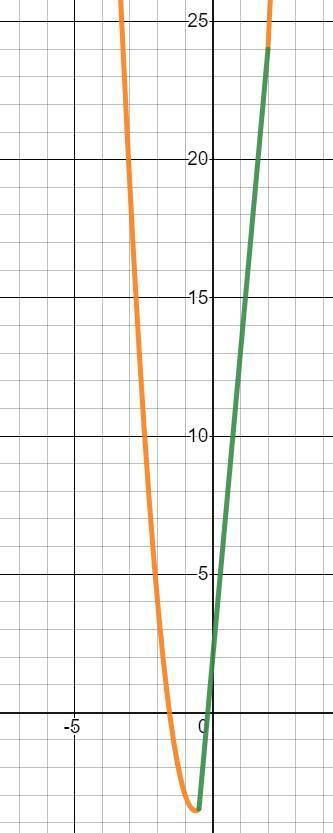
Когда видишь только буквы a (параметр) и x (переменная), то выгодно использовать достаточно универсальный прием: методику построения в координатах (x; a) /или/ (a; x). Тогда у тебя получатся парабола и прямая, склеивающиеся в общих точках (см. прикрепленный файл; построение в координатах (x; a); прямая выделена зеленым; парабола оранжевым). Теперь просто двигаешь горизонтальную прямую вверх и вниз и смотришь пересечения. Единственное решение достигается при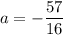 
; решений нет при 
.
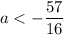2:
Другим хорошим может стать построение левой и правой частей уравнения по-отдельности. Для левой части строим параболу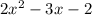 
и симметрично отражаем все, что под осью x. Для правой части будет парабола, которая бегает вверх или вниз в зависимости от значения параметра. Единственное решение возможно, только когда 
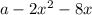касается 
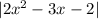, откуда 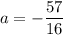. Здесь стоит остановиться на том, как считать a: 
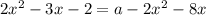(обратите внимание, что здесь можно не писать модуль) 
. Берем дискриминант и приравниваем к нулю: 
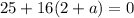. Откуда получаем требуемое значение. Если 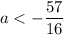, то решений нет.
3:
Пусть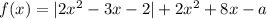 
. Тогда:
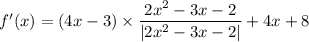. Решив 
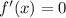, получаем, что 
. Просчитав знаки, делаем вывод, что функция убывает до , а затем возрастает при любом значении параметра. Тогда достаточно решить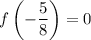 
, откуда 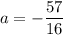. Таким пользоваться не рекомендую.
Задание выполнено!
n! = 1*2**n
n ∈ N
a>b
Aₐᵇ = a! / (a - b)!
Cₐᵇ = a! / (a - b)!b!
Aₓⁿ⁻³ : Aₓⁿ⁻² = x!/(x - n + 3)! : x!/(x - n + 2)! = x!/(x - n + 3)! * (x - n + 2)!/x! = 1 / (x - n + 3)
(x - n + 3)! = 1*2**(x - n + 2)(x - n + 3)
(x - n + 2)! = 1*2**(x - n + 2)
(x - n + 2)! / (x - n + 3)! = (x - n + 3)
Cₓⁿ⁻³ : Cₓⁿ⁻² = x!/(x - n + 3)!(n - 3)! : x!/(x - n + 2)!(n - 2)! = x!/(x - n + 3)!(n - 3)! * (n -2)!(x - n + 2)!/x! = (n - 2) / (x - n + 3)
(n - 2)! = 1*2**(n - 4)(n - 3)(n - 2)
(n - 3)! = 1*2**(n - 4)(n - 3)
(n - 2)! / (n - 3)! = n - 2
1/( x - n + 3) = 1/8
(n - 2)/(x - n + 3) = 5/8
(n - 2) / 8 = 5/8
n - 2 = 5
n = 7
x - n + 3 = x - 7 + 3 = x - 4 = 8
x = 12