В) 5 минут
Пошаговое объяснение:
Дано:
V катера - 1 км за 2 мин = 500 м/мин
V лодки - в 5 раз больше T катера
Расстояние между ними - 3 км = 3 000 м
Найти:
Через сколько они встретятся - ? мин
1) 1 · 5 = 5 (мин) - Столько времени тратит лодка на 500 м.
2) 500 : 5 = 100 (м/мин) - V лодки
3) 100 + 500 = 600 (м/мин) - V сближения
T = S : V (T - время, S - расстояние, V - скорость
4) 3 000 : 600 = 5 (мин) - T через которое они встретятся
Теперь посмотрим варианты ответов:
А) 2 мин
Б) 3 мин
В) 5 мин
Г) 6 мин
В) 5 минут
Формула, устанавливающая зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то S₁ = 7,2 (см²)
2) если h = 2, то S₂ = 7,2h = 14,4 (см²)
1) если h = 3,6, то S₃ = 7,2h = 25,92 (см²)
Пошаговое объяснение:
Требуется записать формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h. Пользуясь формулой, вычисли S, если h = 1; 2; 3,6.
Площадь боковой поверхности параллелепипеда найдем по формуле:
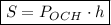 , где Р - периметр основания, h - высота.
, где Р - периметр основания, h - высота.
По условию Росн. = 7,2 см.
Составим формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то
S₁ = 7,2h = 7,2 · 1 = 7,2 (см²)
2) если h = 2, то
S₂ = 7,2h = 7,2 · 2 = 14,4 (см²)
1) если h = 3,6, то
S₃ = 7,2h = 7,2 · 3,6 = 25,92 (см²)
Пошаговое объяснение:
Числа зі знаком «–», наприклад –2; –1,5 називають від’ємними числами.
Числа зі знаком «+», наприклад +5; +4,7 – називають додатними числами.
Число 0 не є ані додатним, ані від’ємним.
У запису додатних чисел знак «+», як правило не ставиться, наприклад, замість +6 записують 6. Отже, числа +6 і 6 не відрізняються одне від одного: +6 = 6.
Числа, які використовують під час лічбі, називають натуральними числами.
Два числа, що відрізняються одне від одного лише знаками, називають протилежними числами.
Число 2 протилежне число –2 і , навпаки число –2 протилежне числу 2.
Натуральні числа, протилежні ім. числа і число 0 – називають цілими числами.
Цілі числа (додатні, від’ємні і число 0) та дробові числа (додатні, від’ємні) називають раціональними числами.
1) від’ємні числа: -1,8; -4; -13.
2) додатні числа: 57; 0,55; 10; 0,0001.
3) цілі числа: 57; -4; 10; -13.
4) раціональні числа: -1,8; 57; 0,55; -4; 10; -13; 0,0001.