
Пошаговое объяснение:
97.
б) x÷(-3)+3≥-6; x÷(-3)≥-6-3; x≤-9·(-3); x≤27; x∈(-∞; 27]
////////////////////////////
---------------------------.--------------------------->x
27
д) x÷(-2)+8<-1; x÷(-2)<-1-8; x>-9·(-2); x>18; x∈(18; +∞)
/////////////////////
---------------------------°-------------------->x
18
з) x÷(-4)+4≤-4; x÷(-4)≤-4-4; x≥-8·(-4); x≥32; x∈[32; +∞)
///////////////////////
------------------.--------------------->x
32
99.
б) x/(-2) -1<2; x/(-2)<2+1; x>3·(-2); x>-6; x∈(-6; +∞)
д) y/(-8) +3≥-2; y/(-8)≥-2-3; y≤-5·(-8); y≤40; y∈(-∞; 40]
з) z/(-7) +3<7; z/(-7)<7-3; z>4·(-7); z>-28; z∈(-28; +∞)
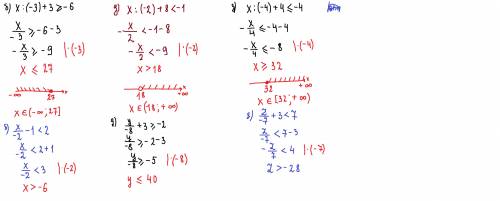
Примем за х количество километров, пройденных за первый день.
Во второй день указанно, что он 120 %, это значит, что он 1,2 * х км. В третий день 2/3 * (1,2 * х) км.
Преобразуем выражение.
2/3 * 1,2 * х = 2/3 * 12/10 * х = 2/3 * 6/5 * х = 4/5 * х = 8/10 * х = 0,8 * х.
Сложим путь за все четыре дня и составим уравнение.
х + 1,2 * х + 0,8 * х + 28 = 103.
(1 + 1,2 + 0,8) * х = 103 - 28.
3 * х = 75.
х = 75 : 3.
х = 25 км лыжник в первый день.
1,2 * 25 = 30 км - во второй день.
0,8 * 25 = 20 км - в третий день.
ответ: 25 км в первый день, 30 км - во второй день, 20 км в третий день.
а) (-3) + (-4) + 6 = -7 + 6 = -1
б) (-6) - 2 - (-3) = -8 + 3 = -5
с) 8 - 5 + 2 = 3 + 2 = 5
д) - 10 - 4 + 12 + 3 = -14 + 12 + 3 = -2 + 3 = 1
е) 8 - 7 + 2 - 11 - 7 = 1 + 2 - 11 - 7 = 3 - 11 - 7 = -8 - 7 = -15