Длина пути от вершины до нижней точки горки 16 м.
Пошаговое объяснение:
Надо найти путь, который проезжает девочка от вершины горки до ее нижней точки.
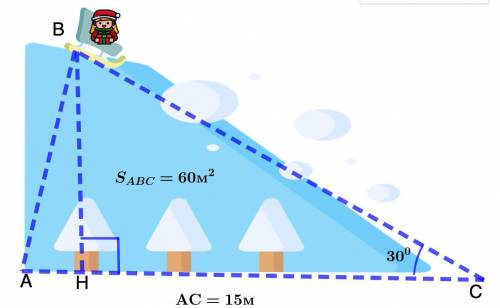
Дано: ΔАВС.
ВH - высота;
АС = 15 м; ∠С = 30°;
S = 60 м²
Найти: ВС.
Чтобы найти длину горки, нужно сначала найти ее высоту.
1. Найдем высоту горки.
Воспользуемся формулой площади треугольника:
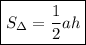 ,
,
где а - основание; h - высота.
Подставим в формулу данные значения:
S = 60 м²; а = 15 м; h = ВH
Получим:
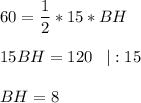 .
.
⇒ высота горки 8 м.
Зная высоту, можем найти длину горки.
2. Найдем длину пути, которое проехала девочка.
Рассмотрим ΔHВС - прямоугольный.
В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы.
⇒ ВС = 2 · ВН
ВС = 8 · 2 = 16 (м)
Пошаговое объяснение:
1) y=x²+4x-12=x²+4x+4-4-12=(x+2)²-16 это парабола у=x² смещенная на 2 единицы вправо и на 16 вниз
наименьшее значение функции -16
2) координаты вершины
х₀=-b/2a=4/14=2/7
y₀=7*(2/7)²-4*2/7=(4/7)-(8/7) =-4/7 наименьшее значение
3) y=-3x² 'это парабола y=-3x² симметрично отображенная относительно оси ОХ