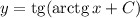Y = x² - парабола (на рисунке синяя линия)
х = 3 - прямая перпендикулярная оси абсцисс, проходящая через точку (3,0) (зелёная линия на рисунке)
y = 0 - прямая, совпадающая с осью абсцисс (красная линия на рисунке)
Найдём ещё одну прямую, которая ограничивает параболу по иксу. Для этого в уравнение параболы подставляем y=0 и решаем уравнение относительно икса: x = 0 - ещё одна прямая перпендикулярная оси абсцисс (левая зелёная линия).
В итоге получается область серого цвета, площадь которой надо найти. Площадь находится с определённого интеграла от параболы в пределах от х=0 до х=3 (это будут пределы интегрирования).
Пошаговое объяснение:
ОБЩЕЕ у всех трех функций.
1. Функция второго порядка - парабола.
2. Область определения - все действительные числа.
D(x)∈(-∞;+∞). Непрерывная, разрывов нет,
ДАНО: -2*х² - х +3.
1. Точки пересечения с осью Х - корни функции - решаем квадратное уравнение. D=25,
x1 = - 1.5, [2 = 1.
2. Промежутки знакопостоянства. Коэффициент при х² < 0 - ветви параболы ВНИЗ.
Положительна - между корней.
3. Первая производная - y'(x) = -4*x - 1. Корень производной: х = - 0,25.
4. Экстремум: максимум - Y(-0.25) = 3.125
5. Возрастает: Х∈(-∞;-0,25], убывает: Х∈[-0.25;+∞)
5. Рисунок к задаче в приложении.
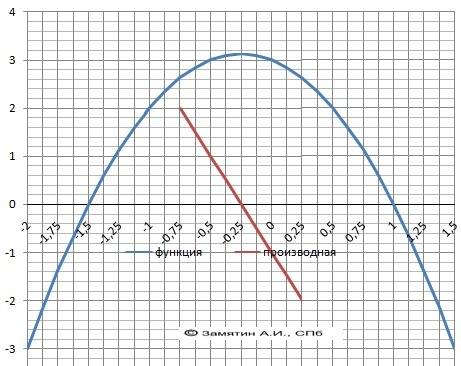
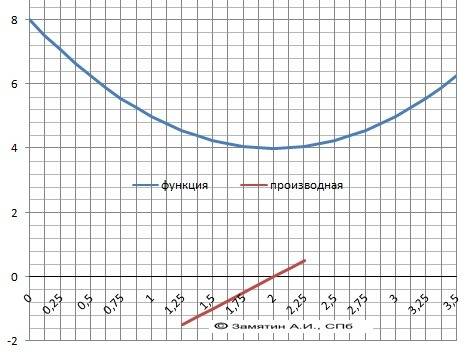
Функция 2.
y =(x-2)² + 4 = x² - 4*x + 8
Корней - нет.
ответ: