Введу некоторые поправки: сумма начинается с n = 1.
Степенной ряд в общем виде записывается следующим образом: , где - формула числовых коэффициентов. Для данного ряда: . Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу Теперь нужно проверить сходимость ряда на концах этого интервала.
Если имеем - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется. Таким образом, предложенный рассматриваемый ряд сходится. Теперь нужно проверить на условной и абсолютной сходимости ряда. Возьмём ряд по модулю: - сходящийся ряд. Следовательно, ряд сходится абсолютно, значит — точка сходимости.
Аналогично, если , имеем — сходящийся ряд. Следовательно,
Таким образом, данный степенной ряд является сходящимся при
1. Зная рост сестры, мы можем определить как прыгнул Женя, на какую высоту. 105 см+10 см = 115 см Теперь 115 см + 34 см = 149 см - рост Жени
2. Найдем общую площадь огорода: 80*35 = 2800 Затем 2800-2240 = 560 квадратных метров
3. 24*6 = 144 см - длина Находим перимитр прямоугольника: (144+24)*2= 336 Зная P прямоуг, найдем сторону квадратного участка: 336/4 = 84 см
4. 1)4+3=7 частей-смородины и крыжовника 2)560:7=80 грамм-1 часть 3)4*80=320 грамм-смородины. 4)3*80=240 грамм-крыжовника. 5)2*80=160 грамм-малины 6)320+240+160=720 грамм ягод взяли для компота
Введу некоторые поправки: сумма начинается с n = 1.
Степенной ряд в общем виде записывается следующим образом: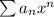 , где
, где 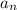 - формула числовых коэффициентов. Для данного ряда:
- формула числовых коэффициентов. Для данного ряда: 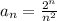 . Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
. Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу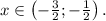 Теперь нужно проверить сходимость ряда на концах этого интервала.
Теперь нужно проверить сходимость ряда на концах этого интервала.
Если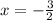 имеем
имеем 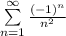 - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
- числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется. Таким образом, предложенный рассматриваемый ряд сходится. Теперь нужно проверить на условной и абсолютной сходимости ряда. Возьмём ряд по модулю: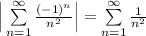 - сходящийся ряд. Следовательно, ряд
- сходящийся ряд. Следовательно, ряд 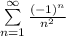 сходится абсолютно, значит
сходится абсолютно, значит 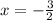 — точка сходимости.
— точка сходимости.
Аналогично, если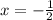 , имеем
, имеем 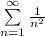 — сходящийся ряд. Следовательно,
— сходящийся ряд. Следовательно,
Таким образом, данный степенной ряд является сходящимся при![x \in [-\frac{3}{2};-\frac{1}{2}].](/tpl/images/1356/8046/1421e.png)