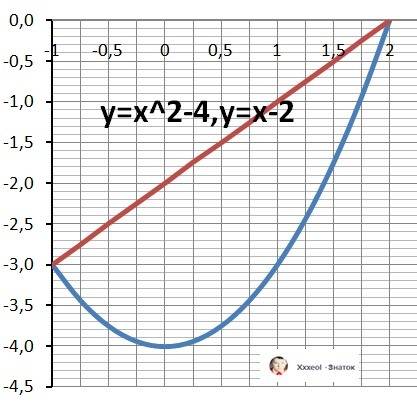
ДАНО: Y = x² - 4, Y = x - 2
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
Площадь фигуры - интеграл разности функций.
1. Находим пределы интегрирования - находим точки пересечения.
У1 =х² - 4 = У2 = х - 2
х² - х - 2 = 0 - решаем квадратное уравнение - это и есть разность функций.
b = - 1 - нижний предел, a = 2 - верхний предел.
2, Записываем разность функций - в обратном порядке и интегрируем.
s(x) = 2 - x - x² - интегрируем - находим первообразную.
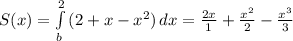
Лично мне нравится такая запись интеграла - понятно как получаются коэффициенты.
3. Вычисляем значения подставив пределы интегрирования.
S(2) = 4 +2 - 2 2/3 = 3 1/3 - подставили верхний предел
S(-1) = - 2 + 1/2 - 1/3 = - 1 1/6 - подставили нижний предел
S = S(2) - S(-1) = 3 1/3 - 1 1/6 = 4 1/2 = 4.5 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
ответ: - 5целых 61/161
Пошаговое объяснение:
( 2,8 - 1целая 2/3 ) * ( - 4целых 2/7 ) + 2целых 2/5 : ( - 4,6 ) = - 5целых 61/161
1) 2,8 - 1целая 2/3 = 2целых 4/5 - 1целая 2/3 = 2целых 12/15 - 1целая 10/15 = 1целая 2/15
2) 1целая 2/15 * ( - 4целых 2/7 ) = 17/15 * ( - 30/7 ) = 17/1 * ( - 2/7 ) = - 34/7 = - 4целых 6/7
3) 2целых 2/5 : ( - 4,6 ) = 2целых 2/5 : ( - 4целых 3/5 ) = 12/5 : ( - 23/5 ) = 12/5 * ( - 5/23 ) = 12/1 * ( - 1/23 ) = - 12/23
4) - 4целых 6/7 + ( - 12/23 ) = - 4целых 138/161 + ( - 84/161 ) = - 4целых 222/161 = - 5целых 61/161
Правильный ответ: с) 153<а<161