Раз некоторое число удовлетворяет уравнению при любом , то оно также удовлетворяет уравнению при .
То есть, если мы подставим в уравнение , то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при ): с обеих сторон в первом случае получается , а во втором (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при . И если ответ на задачу существует, то он может быть только , или и , и . Но про другие значения мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при :
Вот только первый логарифм не всегда существует. может быть отрицательным (возьмите, к примеру, ). А подлогарифмическое выражение обязано быть положительным. Значит, такой нас не устраивает.
Теперь проверим :
В обеих частях мы получили (так как , если ). Также , поэтому все ограничения будут выполняться.
Я в розетку суну рожки И поеду по дорожке. А за мной такая гладь: Ни морщинки не видать. Я хозяйкин лучший друг - Электрический ... (утюг) (в тексте также присутствует слово "розетка")
Если в доме пахнет газом, Вызывай на сразу! Ведь отряд Вам конечно, рад. И свяжись без промедленья, Ты со... (службою в загадке также есть слово "газ")
Не вода, не суша – на лодке не уплывешь и ногами не пройдешь. (болото)
Без родителей опасность Запрещает там ходить. Даже слабую старушку Нужно за руку водить. (проезжая часть)
Я тряпка не простая: Ведь я все буквы знаю! И цифры знаю тоже, Их ровно десять штук! Я здорово считаю, Могу сложить, умножить. Писать вот не умею, Поскольку нету рук. (тряпка для вытирания доски)
Белый он, как снег, колючий. Как песок сухой, сыпучий. Сладкий-сладкий, словно мёд. Чай с ним часто муха пьёт. (сахар)
Раз некоторое число
удовлетворяет уравнению при любом 
, то оно также удовлетворяет уравнению при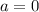 
.
То есть, если мы подставим в уравнение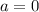
, то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при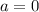
): с обеих сторон в первом случае получается 
, а во втором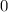 
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при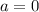
. И если ответ на задачу существует, то он может быть только 
, 
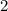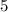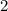или и 
, и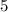 
. Но про другие значения 
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при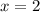
:
Вот только первый логарифм не всегда существует.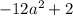
может быть отрицательным (возьмите, к примеру, 
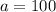). А подлогарифмическое выражение обязано быть положительным. Значит, такой 
нас не устраивает.
Теперь проверим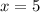
:
В обеих частях мы получили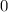
(так как 
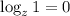, если 
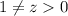). Также 
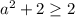, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: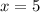
.
Задача решена!