Правильная четырёхугольная пирамида.
Сторона основания = 12.
Высота пирамиды = 8.
Найти:Апофема пирамиды - ?
Решение:Обозначим правильную четырёхугольную пирамиду буквами SABCD.
AB - сторона основания ⇒ AB = 12.
SO - высота пирамиды ⇒ SO = 8.
Т.к. данная пирамида - правильная четырёхугольная ⇒ основание этой пирамиды - квадрат.
Квадрат - это геометрическая фигура, у которой все стороны равны.
⇒ АВ = ВС = CD = AD = 12.
Обозначим точку К на стороне ВС.
Проведём апофему SK из вершины пирамиды S к точке К.
Апофема - высота боковой грани правильной пирамиды, проведённая из вершины этой пирамиды.
Апофема, проведённая из вершины правильной пирамиды к стороне основания этой пирамиды, делит эту сторону на две равные части.
Катет прямоугольного треугольника, образованный апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины стороны основания правильной пирамиды.
ОК - образованный катет ⇒ ОК = 1/2AB(CD, AD, BC) = 12/2 = 6.
ΔSOK - прямоугольный, так как SO - высота пирамиды.
Найдём апофему SK, по теореме Пифагора: (с = а² + b², где с - гипотенуза; a, b - катеты).
SK = √(SO² + OK²) = √(8² + 6²) = √(64 + 36) = √100 = 10 ед.
ответ: 10 ед.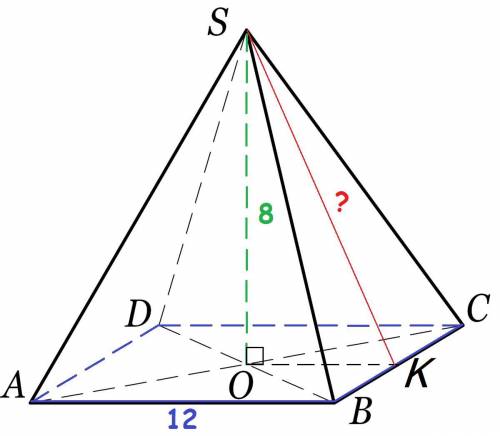
В быту, в учебных мастерских и на производственных предприятиях учащимся приходится сталкиваться с выражением чисел, обозначающих длину, массу, стоимость и другие величины, десятичной дробью и наоборот. Начать изучение этой темы следует с выражения мер длины стоимости и массы десятичной дробью и наоборот. Например, 1 дм — это одна десятая доля метра, следовательно, 1 дм=0,1 м. На основании этого можно составить такую табличку:
1 дм=0,1 м
2 дм=0,2 м
5 дм=0,5 м
15 дм =1,5 м, так как 10 дм — это целый метр.
По аналогии с этим можно провести рассуждения и записать десятичными дробями числа, выраженные в других мерах. Например: 326
1 к.=0,01 р. 2 к.=0,02 р. 15 к.=0,15 р. 125 к. = 1,25 р.
1 г=0,001 кг
5 г=0,005 кг
18 г=0,018 кг
235 г=0,235 кг
При записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью следует соблюдать определенную последовательность, учитывая степень трудности выражения этого числа десятичной дробью. Вначале следует предлагать учащимся числа, выраженные одной единицей мер длины, стоимости, массы и др., а затем — двумя, причем вначале единичное отношение мер должно равняться 10. Например:
2 дм=0,2 м 3 см=0,3 дм 7 мм=0,7 см
3 м 5 дм=3,5 м
7 дм 5 см=7,5 дм
1 см 8 мм=1,8 см и т.д.
Затем надо брать такие числа, где единичное отношение мер равно 100. Например:
1 м 12 см=1,12 м8 р. 75 к. = 8,75 р. 3 ц 8 кг=3,08 ц
1 см=0,01 м
5 к.=0,05 р.
25 к.=0,25 р.
Наконец, берутся такие числа, где единичное отношений мер равно 1000. Например:
1 м=0,001 км 2 г=0,002 кг 15 кг=0,015 т
17 км 350 м= 17,350 км
3 кг 725 г=3,725 кг
8 т 600 кг=8,600 т
Особое внимание обращается на такие случаи записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью, в которых в десятичной дроби десятичные доли разряда равны: нулю. Например, при записи десятичной дробью следующих чисел: 8 к., 5 р., 6 к., 3 м 4 см, 7 км 80 м, 8 т 30 кг. Записывается так: 8 к.=0,08 р., так как 1 к.=0,01 р. 5 р. 6 к.=5,06 р.; 3 м4 см = 3,04 м, 7 км 80 см=7,080 км=7,08 км; 8 т 30 кг=8,030 т=8,03 т.
только так сори если не
Пошаговое объяснение:
Скорость катера в стоячей воде, Vс, называют собственной скоростью катера. Следовательно, собственная скорость катера = 1/244 (если это не ошибка в задании)