
Вообще, задачу легко можно представить на диаграмме Эйлер-Венна, но в программе Перспектива (учебники Дорофеев, Миракова, Бука) эти диаграммы не изучались. А вот задачи по ним, почему-то, даются...
Что же, будем решать без построения диаграммы, хотя это было бы очень наглядно и хорошо прояснило бы решение.
Пошаговое объяснение:
1) 100 − 10 = 90 (ч.) - знают какой-либо язык
2) 90 − 75 = 15 (ч.) - знают французский, но не знают немецкого
3) 90 − 83 = 7 (ч.) - знают немецкий язык, но не знают французского
4) 90 − (15 + 7) = 90 − 22 = 68 (ч.) - знают оба языка
ответ: 68 туристов знали оба языка.


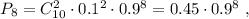

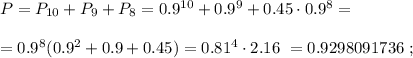
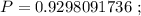
Выражение 1.
(700 074 - 269 574) : (3090 + 6560 : 16) = 123
1) 700 074 - 269 574 = 430 500
2) 6560 : 16 = 410
3) 3090 + 410 = 3500
4) 430 500 : 3500 = 123
ответ: 123
Выражение 2.
(348 577 - 740 160 : 72 * 30) * 23 - 487 582 = 436 489
1) 740 160 : 72 = 10 280
2) 10 280 * 30 = 308 400
3) 348 577 - 308 400 = 40 177
4) 40 177 * 23 = 924 071
5) 924 071 - 487 582 = 436 489
ответ: 436 489
Выражение 3.
5300 * 62 - (800 007 - 697 498) + (24 * 350 + 147 986) = 382 477
1) 800 007 - 697 498 = 102 509
2) 24 * 350 = 8400
3) 8400 + 147 986 = 156 386
4) 5300 * 62 = 328 600
5) 328 600 - 102 509 = 226 091
6) 226 091 + 156 386 = 382 477
ответ: 382 477
68 человек знает французский и немецкий