1. Определим массу металлолома, собранного 6-А классом, если известно, что они собрали 3/8 от 264 кг металлолома:
264 * 3/8 = 33 * 3 = 99 кг.
2. Теперь определим, какое количество приходится на остальные два класса, которые тоже собирали металлолом, для этого отнимем от массы всего собранного металлолома, вес металлолома, собранного 6-А классом:
264 - 99 = 165 кг.
3. По условию задачи 6-Б собрал 7/15 от 165 кг, вычислим и это значение:
165 * 7/15 = 11 * 7 = 77 кг.
4. Наконец, выясним массу металлолома, что собрал 6-В класс, отняв от всего собранного металлолома вес того металлолома, что собрали 6-А и 6-Б классы:
264 - 99 - 77 = 165 - 77 = 88 кг.
ответ: получили, что 6-В класс собрал 88 кг металлолома.
Пошаговое объяснение:
надеюсь тебе:)
Для удобства нарисуем такую диаграмму (см. вложение).
Напишем в соединении "колец" 18 - это те, кто писал олимпиаду и по математике, и по русскому.
Всего по математике приняли участие 54 человека. Из них 18 писали и русский. Значит, чтобы узнать количество учеников, писавших только математику, отнимем: 54-18=36.
По русскому приняли участие 36 человек, из них 18 писали и математику. Значит, чтобы узнать количество учеников, писавших только русский, надо отнять: 36-18=18
Наша диаграмма закончена. Посмотрев на нее, мы видим, что математику писало 36 человек, русский – 18 человек, а оба предмета – 18 человек.
Чтобы найти общее количество участников, прибавим: 36+18+18=72.
ответ: 72 человека участвовали в олимпиаде.
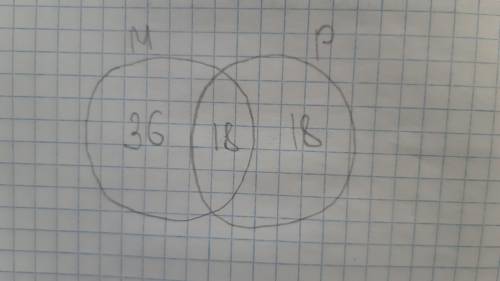
Прямоугольник — четырёхугольник, у которого все углы прямые. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°.